题目内容
(本小题满分13分) 已知函数 .
.
(Ⅰ)若函数在区间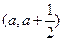 其中a >0,上存在极
其中a >0,上存在极 值,求实数a的取值范
值,求实数a的取值范 围;
围;
(Ⅱ)如果当 时,不等式
时,不等式 恒成立,求实数k的取值范围;
恒成立,求实数k的取值范围;
 .
.
(Ⅰ)若函数在区间
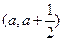 其中a >0,上存在极
其中a >0,上存在极 值,求实数a的取值范
值,求实数a的取值范 围;
围;(Ⅱ)如果当
 时,不等式
时,不等式 恒成立,求实数k的取值范围;
恒成立,求实数k的取值范围;解:(Ⅰ)因为
 , x >0,则
, x >0,则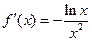 ,
,
当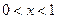 时,
时,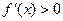 ;当
;当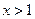 时,
时,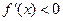 .
.
所以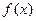 在(0,1)上单调递增;在
在(0,1)上单调递增;在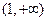 上单调递减,
上单调递减,
所以函数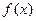 在
在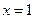 处取得极大值.
处取得极大值.
因为函数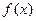 在区间
在区间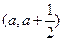 (其中
(其中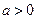 )上存在极值,
)上存在极值,
所以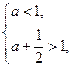 解得
解得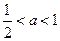 .
.
(Ⅱ)不等式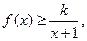 即为
即为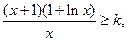 记
记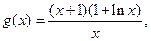
所以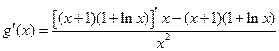

令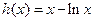 ,则
,则
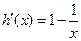 ,
,
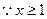 ,
, 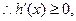
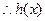 在
在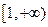 上单调递增,
上单调递增,
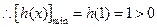 ,从而
,从而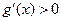 ,
,
故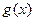 在
在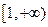 上也单调递增, 所以
上也单调递增, 所以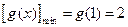 ,所以
,所以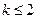

 , x >0,则
, x >0,则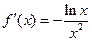 ,
,当
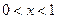 时,
时,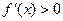 ;当
;当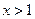 时,
时,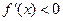 .
.所以
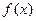 在(0,1)上单调递增;在
在(0,1)上单调递增;在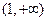 上单调递减,
上单调递减,所以函数
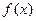 在
在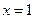 处取得极大值.
处取得极大值. 因为函数
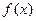 在区间
在区间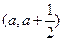 (其中
(其中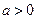 )上存在极值,
)上存在极值,所以
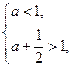 解得
解得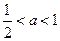 .
. (Ⅱ)不等式
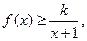 即为
即为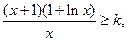 记
记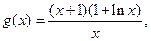
所以
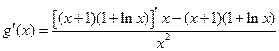

令
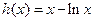 ,则
,则
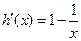 ,
, 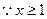 ,
, 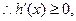
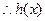 在
在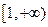 上单调递增,
上单调递增, 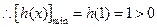 ,从而
,从而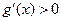 ,
,故
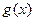 在
在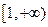 上也单调递增, 所以
上也单调递增, 所以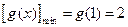 ,所以
,所以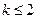
略

练习册系列答案
相关题目


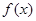 在[1,
在[1, 上递增,求
上递增,求 的取值范围;
的取值范围;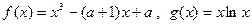 .
.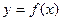 ,
,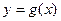 在
在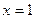 处的切线相互垂直,求这两个切线方程;
处的切线相互垂直,求这两个切线方程;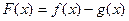 单调递增,求
单调递增,求 的取值范围.
的取值范围.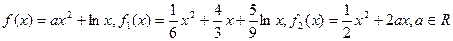 .
.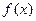 在点
在点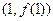 处的切线恒过定点,并求出定点坐标;
处的切线恒过定点,并求出定点坐标;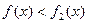 在区间
在区间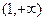 上恒成立,求
上恒成立,求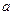 的取值范围;
的取值范围;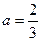 时,求证:在区间
时,求证:在区间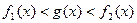 恒成立的函数
恒成立的函数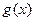
 是一个三次函数,
是一个三次函数,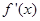 为其导函数.如图所示是函数
为其导函数.如图所示是函数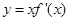 的图像的一部分,则
的图像的一部分,则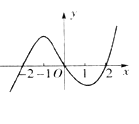
 与
与
 与
与
 是函数
是函数 的一个极值点,其中
的一个极值点,其中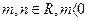
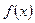 的单调区间
的单调区间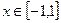 时函数
时函数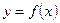 的图象上一任意点的切线斜率恒大于3m,求m的取值范围
的图象上一任意点的切线斜率恒大于3m,求m的取值范围 是定义
是定义 在R上的奇函数,当
在R上的奇函数,当 时,
时, ,且
,且 ,
, 的解集为 ▲
的解集为 ▲  在点
在点 处的切线方程为( )
处的切线方程为( )


