题目内容
(12分)设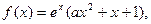
(1)当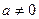 时,求:函数
时,求:函数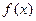 的单调区间;
的单调区间;
(2)若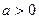 时,求证:当
时,求证:当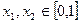 时,不等式
时,不等式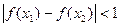
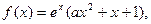
(1)当
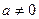 时,求:函数
时,求:函数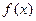 的单调区间;
的单调区间;(2)若
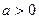 时,求证:当
时,求证:当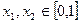 时,不等式
时,不等式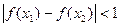
解:(Ⅰ)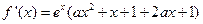 .
.
因为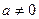 于是
于是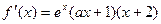 .
.
所以当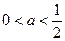 时,
时, ,使
,使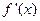 <0
<0
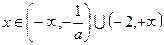 使
使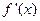 >0
>0
当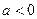 时,
时,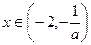 时使
时使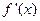 >0.
>0.
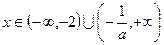 时,使
时,使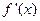 <0
<0
当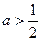 时,
时,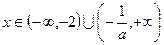 时,使
时,使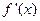 >0.
>0.
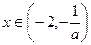 时,使
时,使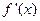 <0
<0
当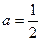 时,
时,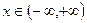 时,使
时,使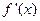 >0.
>0.
从而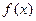 的单调性满足:
的单调性满足:
当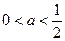 时,在
时,在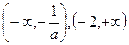 上单调增加,在
上单调增加,在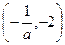 上单调减少;
上单调减少;
当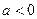 时,在
时,在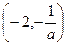 上单调增加,在
上单调增加,在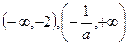 上单调减少;
上单调减少;
当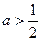 时,在
时,在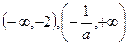 上单调增加,在
上单调增加,在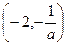 上单调减少;
上单调减少;
当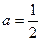 时,在
时,在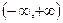 上单调增加
上单调增加
(2)由(Ⅰ)知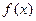 在
在 单调增加,
单调增加,
故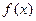 在
在 的最大值为
的最大值为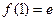 ,最小值为
,最小值为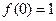 .
.
从而当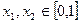 时,不等式
时,不等式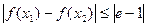
所以当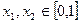 时,不等式
时,不等式 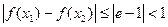
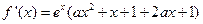 .
.因为
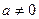 于是
于是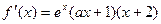 .
.所以当
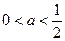 时,
时, ,使
,使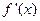 <0
<0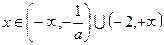 使
使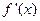 >0
>0当
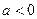 时,
时,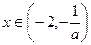 时使
时使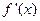 >0.
>0.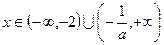 时,使
时,使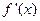 <0
<0当
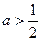 时,
时,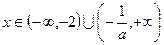 时,使
时,使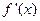 >0.
>0.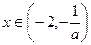 时,使
时,使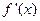 <0
<0当
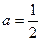 时,
时,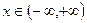 时,使
时,使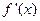 >0.
>0.从而
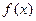 的单调性满足:
的单调性满足:当
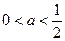 时,在
时,在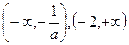 上单调增加,在
上单调增加,在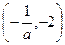 上单调减少;
上单调减少;当
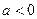 时,在
时,在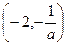 上单调增加,在
上单调增加,在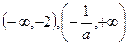 上单调减少;
上单调减少;当
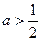 时,在
时,在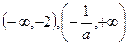 上单调增加,在
上单调增加,在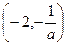 上单调减少;
上单调减少;当
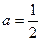 时,在
时,在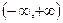 上单调增加
上单调增加(2)由(Ⅰ)知
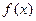 在
在 单调增加,
单调增加,故
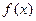 在
在 的最大值为
的最大值为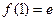 ,最小值为
,最小值为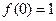 .
. 从而当
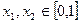 时,不等式
时,不等式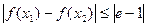
所以当
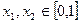 时,不等式
时,不等式 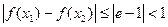
略

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
 (b、c、d为常数),当
(b、c、d为常数),当 时,
时, 只有一个实根,当
只有一个实根,当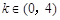 时,
时, 有2个极值点;②函数
有2个极值点;②函数 有一个相同的实根;④
有一个相同的实根;④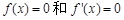 有一个相同的实根。
有一个相同的实根。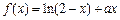 在(0,1)内是增函数.
在(0,1)内是增函数.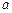 的取值范围;
的取值范围;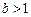 ,求证:
,求证: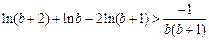 .
. 是一个三次函数,
是一个三次函数,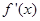 为其导函数.如图所示是函数
为其导函数.如图所示是函数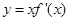 的图像的一部分,则
的图像的一部分,则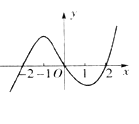
 与
与
 与
与

 ,其图象在
,其图象在 处的切线方程为
处的切线方程为 .
. 的解析式;
的解析式; 的图象与
的图象与 的图象有三个不同的交点,求实数
的图象有三个不同的交点,求实数 的取值范围;
的取值范围; ,若
,若 ,则
,则 ( )
( )



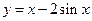 在
在 上的单调递增区间为
上的单调递增区间为  作曲线
作曲线 的切线,则切线斜率为 .
的切线,则切线斜率为 .