题目内容
已知函数f(x)=3x- .
.
(1)若f(x)=2,求x的值;
(2)判断x>0时,f(x)的单调性;
(3)若3tf(2t)+mf(t)≥0对于t∈[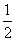 ,1]恒成立,求m的取值范围.
,1]恒成立,求m的取值范围.
解:(1)当x≤0时,f(x)=3x-3x=0,
∴f(x)=2无解.
当x>0时,f(x)=3x-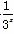 ,令3x-
,令3x-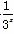 =2.
=2.
∴(3x)2-2·3x-1=0,∴3x=1±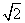 .
.
∵3x>0,∴3x=1-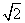 (舍),∴3x=1+
(舍),∴3x=1+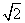 ,
,
∴x=log3(1+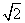 ).
).
(2)当x>0,f(x)=3x-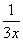 .
.
∵y=3x在(0,+∞)上单调递增,y=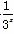 在(0,+∞)上单调递减.
在(0,+∞)上单调递减.
∴f(x)=3x-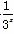 在(0,+∞)上单调递增.
在(0,+∞)上单调递增.
(3)∵t∈ ,∴f(t)=3t-
,∴f(t)=3t-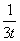 >0.
>0.
∴3tf(2t)+mf(t)≥0化为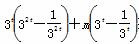 ≥0.
≥0.
即3t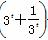 +m≥0,即m≥-32t-1.
+m≥0,即m≥-32t-1.
令g(t)=-32t-1,则g(t)在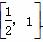 上递减,
上递减,
∴g(x)max=-4.
∴所求实数m的取值范围是[-4,+∞).

练习册系列答案
相关题目
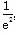 ,都存在x∈R,使得f(x)<m
,都存在x∈R,使得f(x)<m ,x=
,x=


 ,则f(log27)=( )
,则f(log27)=( ) B.
B. C.
C. D.
D.
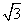 )2+lg
)2+lg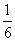 +lg 0.06;
+lg 0.06; (a+b)三向量的终点在同一直线上?
(a+b)三向量的终点在同一直线上?