题目内容
已知函数 (其中
(其中 为常数).
为常数).
(1)当 时,求函数
时,求函数
 的单调区间;
的单调区间;
(2) 当 时,设函数
时,设函数 的3个极值点为
的3个极值点为 ,且
,且 . 证明:
. 证明: .
.
(1) 
令 可得
可得 .列表如下:
.列表如下:
|
|
|
|
|
|
|
| - | - | 0 | + |
|
| 减 | 减 | 极小值 | 增 |
单调减区间为 ,
, ;增区间为
;增区间为 .------------4分
.------------4分
(2)由题,
对于函数 ,有
,有
∴函数 在
在 上单调递减,在
上单调递减,在 上单调递增
上单调递增
∵函数 有3个极值点
有3个极值点 ,
,
从而 ,所以
,所以 ,
,
当 时,
时, ,
, ,
,
∴ 函数 的递增区间有
的递增区间有 和
和 ,递减区间有
,递减区间有 ,
, ,
, ,
,
此时,函数 有3个极值点,且
有3个极值点,且 ;
;
∴当 时,
时, 是函数
是函数 的两个零点,————8分
的两个零点,————8分
即有 ,消去
,消去 有
有
令 ,
, 有零点
有零点 ,且
,且
∴函数 在
在 上递减,在
上递减,在 上递增
上递增
要证明 





 即证
即证

构造函数 ,
, =0————10分
=0————10分
只需要证明 单调递减即可.而
单调递减即可.而 ,
,
 在
在 上单调递增,
上单调递增, 

练习册系列答案
相关题目






 ,则
,则 的值为( )
的值为( ) B.
B. C.
C. D.
D.

 ,
, .
.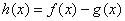 ,求
,求 的单调区间;
的单调区间; ,总有
,总有 成立.
成立.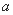 的取值范围;
的取值范围; ,不等式
,不等式
 恒成立.
恒成立. (
( 为奇函数,且函数
为奇函数,且函数 的图象的两相邻对称轴之间的距离为
的图象的两相邻对称轴之间的距离为 .
. 的值;(2)将函数
的值;(2)将函数 个单位后,得到函数
个单位后,得到函数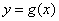 的图象,求函数
的图象,求函数 的单调递增区间.
的单调递增区间.  的值的程序框图,
的值的程序框图, B.
B. C.
C. D.
D.

 ,若直线
,若直线 与圆
与圆 相切,且切点在第二象限,则实数
相切,且切点在第二象限,则实数 .
. 时,则该程序运行后输出的结果是
时,则该程序运行后输出的结果是
 表示的点落在 ( )
表示的点落在 ( )