题目内容
已知函数 ,
, .
.
(Ⅰ)设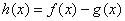 ,求
,求 的单调区间;
的单调区间;
(Ⅱ)若对 ,总有
,总有 成立.
成立.
(1)求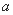 的取值范围;
的取值范围;
(2)证明:对于任意的正整数 ,不等式
,不等式
 恒成立.
恒成立.
解:(Ⅰ)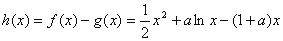 ,定义域为
,定义域为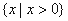 ,
,
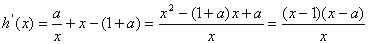 , …… 1分
, …… 1分
(1)当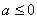 时,令
时,令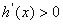 ,
,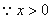 ,
,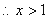 ,
,
令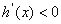 ,
, 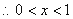 ;
;
(2)当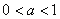 时,令
时,令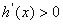 ,则
,则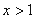 或
或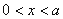 ,
,
令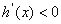 ,
, 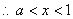 ; …… 3分
; …… 3分
(3)当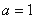 时,
时,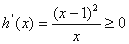 恒成立;
恒成立;
(4)当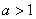 时,令
时,令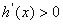 ,则
,则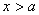 或
或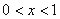 ,
,
令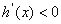 ,
, 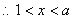 ; …… 4分
; …… 4分
综上:当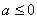 时,
时, 的增区间为
的增区间为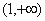 ,
, 的减区间为
的减区间为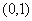 ;
;
当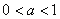 时,
时, 的增区间为
的增区间为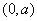 和
和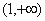 ,
, 的减区间为
的减区间为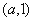 ;
;
当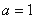 时,
时, 的增区间为
的增区间为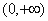 ;
;
当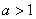 时,
时, 的增区间为
的增区间为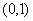 和
和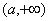 ,
, 的减区间为
的减区间为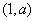 . ……5分
. ……5分
(Ⅱ)(1)由题意,对任意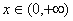 ,
,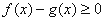 恒成立,即
恒成立,即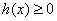 恒成立,
恒成立,
只需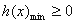 . ……6分
. ……6分
由第(Ⅰ)知:
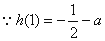 ,显然当
,显然当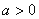 时,
时, 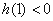 ,此时对任意
,此时对任意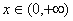 ,
,
不能恒成立; (或者分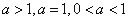 逐个讨论) …… 8分
逐个讨论) …… 8分
当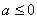 时,
时,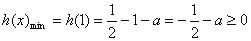 ,
,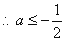 ;
;
综上: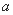 的取值范围为
的取值范围为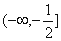 . …… 9分
. …… 9分
(2)证明:由(1)知:当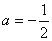 时,
时,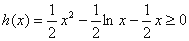 ,……10分
,……10分
即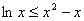 ,当且仅当
,当且仅当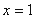 时等号成立.
时等号成立.
当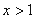 时,可以变换为
时,可以变换为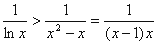 , …… 12分
, …… 12分
在上面的不等式中,令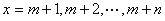 ,则有
,则有

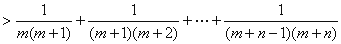
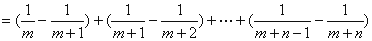
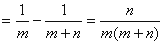
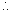 不等式
不等式
 恒成立.
恒成立.

练习册系列答案
相关题目
 是定义在[-1,1]上的奇函数,
是定义在[-1,1]上的奇函数, 时,
时, .
.
 时,
时, .
. 的前
的前 项之和是
项之和是 ,数列
,数列 前
前 ,且
,且 ,则数列
,则数列 中最接近108的项是第 项.
中最接近108的项是第 项.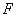 是双曲线
是双曲线 的右焦点,点
的右焦点,点 是该双曲线的左顶点,过
是该双曲线的左顶点,过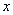 轴的直线与双曲线交于
轴的直线与双曲线交于 两点,若
两点,若 是钝角,则该双曲线的离心率
是钝角,则该双曲线的离心率 的取值范围是
的取值范围是  B.
B. C.
C. D.
D.
 中
中 所对的边分别为
所对的边分别为 ,
, 且
且 .
. 的大小;
的大小; 求
求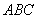 中,
中, 是
是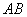 的中点,
的中点, 为线
为线 段
段 上一动点,则
上一动点,则 的取值范围为
的取值范围为  (其中
(其中 为常数).
为常数). 时,求函数
时,求函数
 的单调区间;
的单调区间; 时,设函数
时,设函数 ,且
,且 . 证明:
. 证明: .
. ,方程
,方程 在
在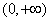 上的解按从小到大的顺序排成数列
上的解按从小到大的顺序排成数列
 .
. ,数列
,数列 的前
的前 项和为
项和为 ,求
,求 是等差数列,
是等差数列, 为其前
为其前 项和,若
项和,若 成等比数列,则
成等比数列,则 。
。