题目内容
20.设f(x)=$\left\{\begin{array}{l}{\frac{sinax}{\sqrt{1-cosx}},-π<x<0}\\{b,x=0}\\{\frac{1}{x}(lnx-ln({x}^{2}+x),x>0}\end{array}\right.$连续,求a,b.分析 问题等价为:$\underset{lim}{x→{0}^{+}}$f(x)=$\underset{lim}{x→{0}^{-}}$f(x)=f(0)=b,再直接求函数在x=0处的左右极限即可.
解答 解:根据题意,$\underset{lim}{x→{0}^{+}}$f(x)=$\underset{lim}{x→{0}^{-}}$f(x)=f(0)=b,
$\underset{lim}{x→{0}^{+}}$$\frac{lnx-ln(x^2+x)}{x}$=$\underset{lim}{x→{0}^{+}}$($\frac{1}{x}-\frac{2x+1}{x^2+x}$)
=$\underset{lim}{x→{0}^{+}}$$\frac{-1}{x+1}$=-1,
因此,b=-1,
又有$\underset{lim}{x→{0}^{-}}$$\frac{sinax}{\sqrt{1-cosx}}$=-$\underset{lim}{x→{0}^{-}}$$\frac{sinax}{\sqrt{2}sin\frac{x}{2}}$
=-$\underset{lim}{x→{0}^{-}}$($\frac{sinax}{ax}$•$\frac{\frac{x}{2}}{sin\frac{x}{2}}$•$\sqrt{2}a$)=-$\sqrt{2}a$,
所以,-$\sqrt{2}a$=-1,a=$\frac{\sqrt{2}}{2}$,
故a=$\frac{\sqrt{2}}{2}$,b=-1.
点评 本题主要考查了函数连续性的应用,涉及函数的左右极限,并考查了运用罗必塔法则求极限,属于中档题.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
8.若sinα=$\frac{k+1}{k-3}$,cosα=$\frac{k-1}{k-3}$,则$\frac{1}{tanα}$的值为( )
| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | -$\frac{3}{4}$ | D. | -$\frac{4}{3}$ |
15. 2015年10月4日,强台风“彩虹”登录广东省湛江市,“彩虹”是1949年以来登陆中国陆地的最强台风,“彩虹”给湛江市人民带来了巨大的财产损失,湛江市教育局调查了湛江市50户居民由于台风造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,作出频率分布直方图,并向全市发出倡议,为受灾的湛江市居民捐款,(视频率为概率)
2015年10月4日,强台风“彩虹”登录广东省湛江市,“彩虹”是1949年以来登陆中国陆地的最强台风,“彩虹”给湛江市人民带来了巨大的财产损失,湛江市教育局调查了湛江市50户居民由于台风造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,作出频率分布直方图,并向全市发出倡议,为受灾的湛江市居民捐款,(视频率为概率)
(Ⅰ)在湛江市受害灾民中随机抽取3户,设损失超过8000元的居民为x户,求x的分布列和数学期望;
(Ⅱ)湛江市教育局调查了50户居民捐款情况如下表,说明是否有95%以上的把握认为捐款数额多于500元和自身经济损失是否超过8000元有关?
 2015年10月4日,强台风“彩虹”登录广东省湛江市,“彩虹”是1949年以来登陆中国陆地的最强台风,“彩虹”给湛江市人民带来了巨大的财产损失,湛江市教育局调查了湛江市50户居民由于台风造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,作出频率分布直方图,并向全市发出倡议,为受灾的湛江市居民捐款,(视频率为概率)
2015年10月4日,强台风“彩虹”登录广东省湛江市,“彩虹”是1949年以来登陆中国陆地的最强台风,“彩虹”给湛江市人民带来了巨大的财产损失,湛江市教育局调查了湛江市50户居民由于台风造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,作出频率分布直方图,并向全市发出倡议,为受灾的湛江市居民捐款,(视频率为概率)(Ⅰ)在湛江市受害灾民中随机抽取3户,设损失超过8000元的居民为x户,求x的分布列和数学期望;
(Ⅱ)湛江市教育局调查了50户居民捐款情况如下表,说明是否有95%以上的把握认为捐款数额多于500元和自身经济损失是否超过8000元有关?
| 经济损失不超过5000元 | 经济损失超过5000元 | 合计 | |
| 捐款超过500元 | 30 | 9 | 39 |
| 捐款不超过500元 | 5 | 6 | 11 |
| 合计 | 35 | 15 | 50 |
9.执行如图所示程序框图,若使输出的结果不大于50,则输入的整数k的最大值为( )
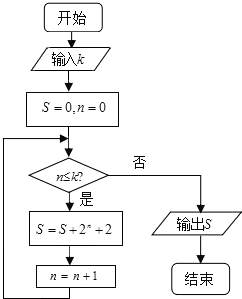

| A. | 4 | B. | 5 | C. | 6 | D. | 7 |