题目内容
(本小题满分13分) 已知等差数列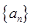 满足:
满足: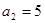 ,
,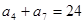 ,
,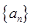 的前n项和为
的前n项和为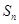 .
.
(Ⅰ)求通项公式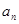 及前n项和
及前n项和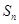 ;
;
(Ⅱ)令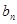 =
=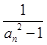 (n
(n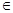 N*),求数列
N*),求数列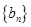 的前n项和
的前n项和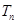 .
.
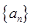 满足:
满足: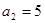 ,
,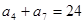 ,
,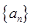 的前n项和为
的前n项和为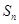 .
.(Ⅰ)求通项公式
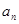 及前n项和
及前n项和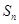 ;
;(Ⅱ)令
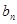 =
=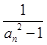 (n
(n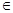 N*),求数列
N*),求数列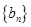 的前n项和
的前n项和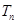 .
.(Ⅰ)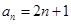 ;
; 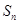 =
=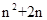 ;(Ⅱ)
;(Ⅱ)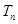 =
=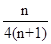 。
。
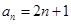 ;
; 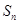 =
=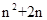 ;(Ⅱ)
;(Ⅱ)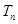 =
=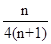 。
。试题分析:(1)结合已知中的等差数列的项的关系式,联立方程组得到其通项公式和前n项和。
(2)在第一问的基础上,得到bn的通项公式,进而分析运用裂项法得到。
解:(Ⅰ)设等差数列
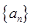 的公差为d,由已知可得
的公差为d,由已知可得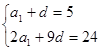 ,
,解得
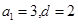 ,……………2分,
,……………2分,所以
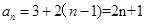 ;………4分
;………4分 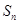 =
=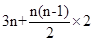 =
=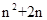 ………6分
………6分(Ⅱ)由(Ⅰ)知
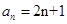 ,
,所以
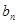 =
=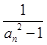 =
=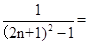
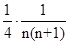 =
=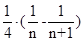 ……10分
……10分所以
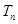 =
=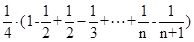 =
=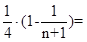
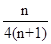
即数列
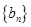 的前n项和
的前n项和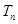 =
=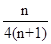 ……13分
……13分点评:解决该试题的关键是能得到等差数列的通项公式,然后求解新数列的通项公式,利用裂项的思想来得到求和。易错点就是裂项的准确表示。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
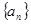 满足
满足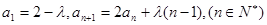
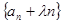 为等比数列;
为等比数列;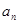 以及前n项和
以及前n项和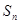 ;
;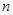 都有
都有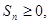 求
求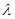 的取值范围。
的取值范围。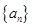 是首项为
是首项为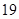 ,公差为
,公差为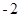 的等差数列.
的等差数列.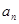 ;
; 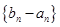 是首项为
是首项为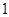 ,公比为
,公比为 的等比数列,求数列
的等比数列,求数列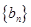 的通项公式及其前
的通项公式及其前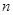 项和
项和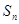 .
.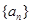 中,
中,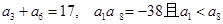 .
.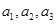 的顺序,使它成为等比数列
的顺序,使它成为等比数列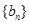 的前三项,求
的前三项,求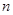 项和.
项和.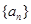 中,前
中,前 项和
项和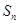 ,且
,且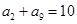 ,则
,则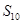 等于( )
等于( )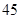



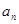 } 是等差数列,且
} 是等差数列,且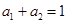 ,
,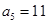 ,则数列{
,则数列{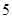 项的和
项的和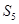 等于( )
等于( )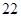
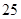
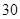
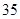
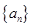 和
和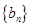 的前
的前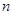 项和分别是
项和分别是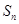 和
和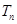 ,已知
,已知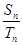 =
=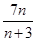 ,则
,则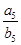 =( )
=( )
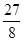
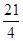
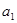 =-2013,
=-2013,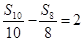 ,则
,则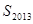 =
=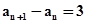 ,则数列
,则数列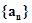 是( )
是( )