题目内容
在△ABC中, a、b、c分别是角A、B、C的对边,△ABC的周长为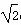 +2,且sinA+sinB=
+2,且sinA+sinB=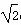 sinC.
sinC.
(1) 求边c的长;
(2) 若△ABC的面积为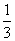 sinC,求角C的度数.
sinC,求角C的度数.
解:(1) 在△ABC中, ∵ sinA+sinB=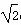 sinC,由正弦定理,得a+b=
sinC,由正弦定理,得a+b=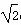 c ,∴ a+b+c=
c ,∴ a+b+c=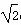 c+c=(
c+c=(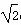 +1)c=
+1)c=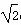 +2.
+2.
∴ a+b=2,c=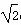 .
.
(2) 在△ABC中, S△ABC= absinC=
absinC=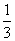 sinC,
sinC,
∴  ab=
ab=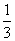 ,即ab=
,即ab= .
.
又a+b=2,在△ABC中,由余弦定理,得cosC= =
= ,又在△ABC中∠C∈(0,π),
,又在△ABC中∠C∈(0,π),
∴ ∠C=60°.

练习册系列答案
相关题目
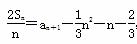 ,n∈N*.
,n∈N*.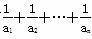 <
<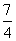 .
. -1)海里的C处的缉私船奉命以10
-1)海里的C处的缉私船奉命以10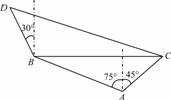
 ,x∈R,A>0,0<φ<
,x∈R,A>0,0<φ<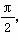 ,y=f(x)的部分图象如图所示,P、Q分别为该图象的最高点和最低点,点P的坐标为(1,A).
,y=f(x)的部分图象如图所示,P、Q分别为该图象的最高点和最低点,点P的坐标为(1,A). ,求A的值.
,求A的值.
 的最小正周期为________.
的最小正周期为________. +θ)=
+θ)= ,则cos2θ=________.
,则cos2θ=________. ,tanβ=-
,tanβ=- ,求2α-β的值.
,求2α-β的值. ,求角C的大小.
,求角C的大小. ,cos(α-β)=
,cos(α-β)= ,且0<β<α<
,且0<β<α< ,求β.
,求β.