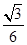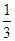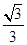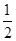题目内容
设A,B分别是直线y= x和y=-
x和y=- x上的动点,且|AB|=
x上的动点,且|AB|=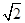 ,设O为坐标原点,动点P满足
,设O为坐标原点,动点P满足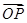 =
=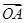 +
+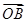 .
.
(1)求点P的轨迹方程;
(2)过点(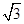 ,0)作两条互相垂直的直线l1,l2,直线l1,l2与点P的轨迹的相交弦分别为CD,EF,设CD,EF的弦中点分别为M,N,求证:直线MN恒过一个定点.
,0)作两条互相垂直的直线l1,l2,直线l1,l2与点P的轨迹的相交弦分别为CD,EF,设CD,EF的弦中点分别为M,N,求证:直线MN恒过一个定点.
 x和y=-
x和y=- x上的动点,且|AB|=
x上的动点,且|AB|=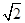 ,设O为坐标原点,动点P满足
,设O为坐标原点,动点P满足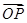 =
=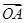 +
+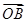 .
.(1)求点P的轨迹方程;
(2)过点(
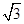 ,0)作两条互相垂直的直线l1,l2,直线l1,l2与点P的轨迹的相交弦分别为CD,EF,设CD,EF的弦中点分别为M,N,求证:直线MN恒过一个定点.
,0)作两条互相垂直的直线l1,l2,直线l1,l2与点P的轨迹的相交弦分别为CD,EF,设CD,EF的弦中点分别为M,N,求证:直线MN恒过一个定点.(1)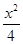 +y2=1(2)见解析
+y2=1(2)见解析
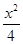 +y2=1(2)见解析
+y2=1(2)见解析(1)设A(x1,y1),B(x2,y2),P(x,y),
∵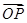 =
=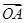 +
+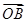 ,∴x=x1+x2,y=y1+y2,
,∴x=x1+x2,y=y1+y2,
∵y1= x1,y2=-
x1,y2=- x2,?
x2,?
∴x=x1+x2=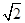 (y1-y2),y=y1+y2=
(y1-y2),y=y1+y2= (x1-x2).
(x1-x2).
∵|AB|=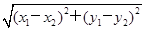 =
=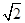 ,∴
,∴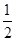 x2+2y2=2,
x2+2y2=2,
∴点P的轨迹方程为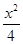 +y2=1.
+y2=1.
(2)证明:设C(x1,y1),D(x2,y2),直线l1的方程为x-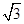 =ky.
=ky.
由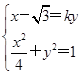 ,得(k2+4)y2+2
,得(k2+4)y2+2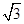 ky-1=0,
ky-1=0,
∴y1+y2=-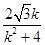 ,x1+x2=
,x1+x2=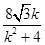 .∴M点坐标为
.∴M点坐标为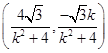 ,
,
同理可得N点坐标为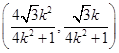 .
.
∴直线MN的斜率kMN=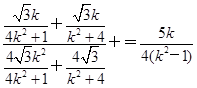 .
.
∴直线MN的方程为y+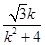 =
=
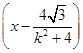 .
.
整理化简得4k4y+(4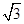 -5x)k3+12k2y-16y+(-20x+16
-5x)k3+12k2y-16y+(-20x+16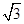 )k=0,
)k=0,
∴x= ,y=0,∴直线MN恒过定点
,y=0,∴直线MN恒过定点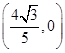
∵
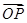 =
=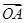 +
+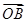 ,∴x=x1+x2,y=y1+y2,
,∴x=x1+x2,y=y1+y2,∵y1=
 x1,y2=-
x1,y2=- x2,?
x2,?∴x=x1+x2=
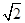 (y1-y2),y=y1+y2=
(y1-y2),y=y1+y2= (x1-x2).
(x1-x2).∵|AB|=
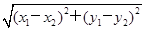 =
=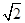 ,∴
,∴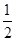 x2+2y2=2,
x2+2y2=2,∴点P的轨迹方程为
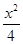 +y2=1.
+y2=1.(2)证明:设C(x1,y1),D(x2,y2),直线l1的方程为x-
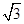 =ky.
=ky.由
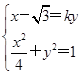 ,得(k2+4)y2+2
,得(k2+4)y2+2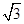 ky-1=0,
ky-1=0,∴y1+y2=-
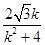 ,x1+x2=
,x1+x2=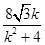 .∴M点坐标为
.∴M点坐标为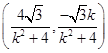 ,
,同理可得N点坐标为
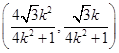 .
.∴直线MN的斜率kMN=
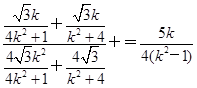 .
.∴直线MN的方程为y+
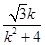 =
=
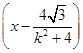 .
.整理化简得4k4y+(4
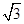 -5x)k3+12k2y-16y+(-20x+16
-5x)k3+12k2y-16y+(-20x+16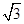 )k=0,
)k=0,∴x=
 ,y=0,∴直线MN恒过定点
,y=0,∴直线MN恒过定点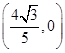

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,向量
,向量 ,经过定点
,经过定点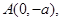 以
以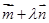 为方向向量的直线与经过定点
为方向向量的直线与经过定点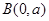 以
以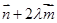 为方向向量的直线相交于
为方向向量的直线相交于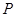 ,其中
,其中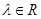 ,
,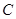 的方程;(2)若
的方程;(2)若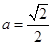 ,过
,过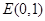 的直线交曲线
的直线交曲线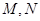 两点,求
两点,求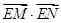 的取值范围。
的取值范围。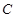 :
: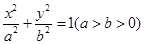 的离心率为
的离心率为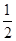 ,右焦点
,右焦点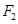 到直线
到直线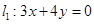 的距离为
的距离为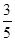 .
. 的方程;
的方程;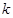 (
(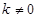 )的直线
)的直线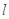 与椭圆
与椭圆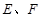 两点,
两点,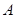 为椭圆的右顶点,直线
为椭圆的右顶点,直线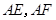 分别交直线
分别交直线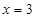 于点
于点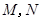 ,线段
,线段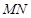 的中点为
的中点为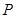 ,记直线
,记直线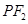 的斜率为
的斜率为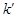 ,求证:
,求证: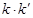 为定值.
为定值.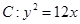 ,点
,点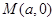 ,过
,过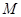 的直线
的直线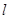 交抛物线
交抛物线 于
于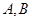 两点.
两点.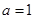 ,抛物线
,抛物线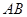 中点的连线垂直于
中点的连线垂直于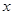 轴,求直线
轴,求直线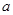 为小于零的常数,点
为小于零的常数,点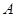 关于
关于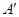 ,求证:直线
,求证:直线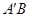 过定点
过定点
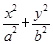 =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e=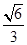 ,一条准线方程为x=
,一条准线方程为x=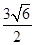
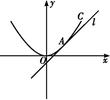
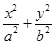 =1(a>b>0)的左、右焦点,A是椭圆C的顶点,B是直线AF2与椭圆C的另一个交点,∠F1AF2=60°.
=1(a>b>0)的左、右焦点,A是椭圆C的顶点,B是直线AF2与椭圆C的另一个交点,∠F1AF2=60°.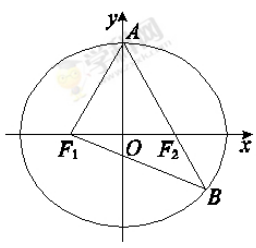
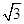 ,求a,b的值.
,求a,b的值.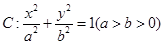 的左、右焦点分别为
的左、右焦点分别为 是
是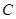 上的点
上的点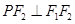 ,
,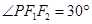 ,则椭圆
,则椭圆