题目内容
11.关于函数f(x)=4sin(2x+$\frac{π}{3}$)(x∈R)有下列命题,其中正确的是②.①y=f(x)的表达式可改写为y=4cos(2x+$\frac{π}{3}$)(x∈R)
②y=f(x)的图象关于点(-$\frac{π}{6}$,0)对称;
③y=f(x)的最小正周期为2π;
④y=f(x)的图象的一条对称轴为x=-$\frac{π}{6}$.
分析 利用诱导公式变形判断①;由f($-\frac{π}{6}$)的值判断②④;求出函数的最小正周期判断③.
解答 解:∵f(x)=4sin(2x+$\frac{π}{3}$)=4cos[$\frac{π}{2}$-(2x+$\frac{π}{3}$)]=4cos(2x-$\frac{π}{6}$),∴①错误;
∵f($-\frac{π}{6}$)=4cos[2×(-$\frac{π}{6}$)-$\frac{π}{6}$]=4cos($-\frac{π}{2}$)=0,∴y=f(x)的图象关于点(-$\frac{π}{6}$,0)对称,故②正确;
函数f(x)=4sin(2x+$\frac{π}{3}$)的最小正周期T=$\frac{2π}{2}=π$,故③错误;
由②知④错误.
故答案为:②.
点评 本题考查命题的真假判断与应用,考查y=Asin(ωx+φ)型函数的图象和性质,是基础题.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
3.某三棱锥的三视图如图所示,且三个三角形均为直角三角形,则三棱锥的体积为( )
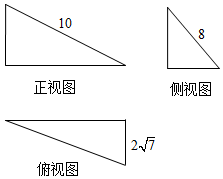

| A. | 32 | B. | $32\sqrt{7}$ | C. | $16\sqrt{7}$ | D. | $64\sqrt{7}$ |
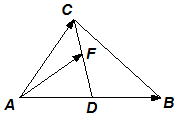 如图所示,在△ABC中,AD=DB,点F在线段CD上,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,$\overrightarrow{AF}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$,则$\frac{1}{x}$+$\frac{4}{y+1}$的最小值为3+2$\sqrt{2}$.
如图所示,在△ABC中,AD=DB,点F在线段CD上,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,$\overrightarrow{AF}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$,则$\frac{1}{x}$+$\frac{4}{y+1}$的最小值为3+2$\sqrt{2}$.