题目内容
2.若平面向量$\vec a=(2,1)$和$\vec b=(x-1,-x)$垂直,则$|\vec a+\vec b|$=$\sqrt{10}$.分析 根据$\overrightarrow{a}⊥\overrightarrow{b}$便可得出$\overrightarrow{a}•\overrightarrow{b}=0$,从而求出x的值,从而得出$\overrightarrow{a}+\overrightarrow{b}$的坐标,进而求出$|\overrightarrow{a}+\overrightarrow{b}|$的值.
解答 解:$\overrightarrow{a}⊥\overrightarrow{b}$;
∴$\overrightarrow{a}•\overrightarrow{b}=2(x-1)+(-x)=0$;
∴x=2;
∴$\overrightarrow{b}=(1,-2)$;
∴$\overrightarrow{a}+\overrightarrow{b}=(3,-1)$;
∴$|\overrightarrow{a}+\overrightarrow{b}|=\sqrt{10}$.
故答案为:$\sqrt{10}$.
点评 考查向量垂直的充要条件,向量数量积的坐标运算,根据向量坐标求向量长度.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
10.函数f(x)=ax+cosx在R上是单调函数,则实数a的取值范围是( )
| A. | [1,+∞) | B. | (1,+∞) | C. | (-∞,-1]∪[1,+∞) | D. | (-∞,-1)∪(1,+∞) |
17.设函数$f(x)=cos(2x-\frac{π}{2})$,x∈R,则f(x)是( )
| A. | 最小正周期为π的奇函数 | B. | 最小正周期为π的偶函数 | ||
| C. | 最小正周期为$\frac{π}{2}$的奇函数 | D. | 最小正周期为$\frac{π}{2}$的偶函数 |
7.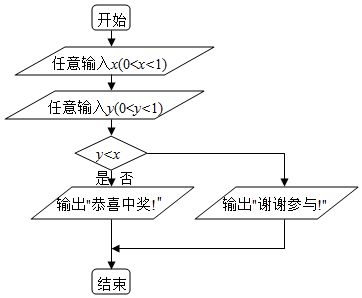 在如图所示程序框图中,任意输入一次x(0≤x≤1)与y(0≤y≤1),则能输出“恭喜中奖!”的概率为( )
在如图所示程序框图中,任意输入一次x(0≤x≤1)与y(0≤y≤1),则能输出“恭喜中奖!”的概率为( )
 在如图所示程序框图中,任意输入一次x(0≤x≤1)与y(0≤y≤1),则能输出“恭喜中奖!”的概率为( )
在如图所示程序框图中,任意输入一次x(0≤x≤1)与y(0≤y≤1),则能输出“恭喜中奖!”的概率为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
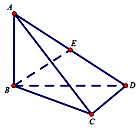 如图:在空间四边形ABCD中,已知AB⊥BC,AB⊥BD,BC⊥CD且AB=BC=6,BD=8,E为AD中点,求异面直线BE与CD所成角.
如图:在空间四边形ABCD中,已知AB⊥BC,AB⊥BD,BC⊥CD且AB=BC=6,BD=8,E为AD中点,求异面直线BE与CD所成角.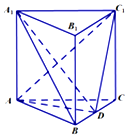 如图,直三棱柱ABC-A1B1C1中,△ABC是等边三角形,D是BC的中点.
如图,直三棱柱ABC-A1B1C1中,△ABC是等边三角形,D是BC的中点.