题目内容
3.某三棱锥的三视图如图所示,且三个三角形均为直角三角形,则三棱锥的体积为( )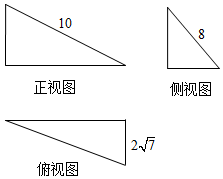
| A. | 32 | B. | $32\sqrt{7}$ | C. | $16\sqrt{7}$ | D. | $64\sqrt{7}$ |
分析 根据三视图复原的几何体是三棱锥,画出图形,
求出正视图中两直角边长,即可计算三棱锥的体积.
解答 解:三视图复原的几何体是三棱锥,底面是直角三角形,一条侧棱垂直底面,
底面直角三角形一直角边长为2$\sqrt{7}$,如图所示,
设正视图中两直角边长分别为a,b,
则a2+b2=102,${(2\sqrt{7})}^{2}$+b2=82,
解得b=6,a=8,
所以三棱锥的体积为:V=$\frac{1}{3}$×$\frac{1}{2}$×8×2$\sqrt{7}$×6=16$\sqrt{7}$.
故选:C.
点评 本题考查了三视图和复原图之间的转换以及三棱锥体积公式的应用问题,是基础题.

练习册系列答案
相关题目
11.若函数f(x)=lnx+ax2-2在区间$({\frac{1}{2},2})$内存在单调递增区间,则实数α的取值范围是( )
| A. | (-∞,-2] | B. | (-2,+∞) | C. | (-2,-$\frac{1}{8}$) | D. | $[-\frac{1}{8},+∞)$ |
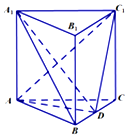 如图,直三棱柱ABC-A1B1C1中,△ABC是等边三角形,D是BC的中点.
如图,直三棱柱ABC-A1B1C1中,△ABC是等边三角形,D是BC的中点.