题目内容
12.已知命题p:指数函数y=(1-a)x是R上的增函数,命题q:不等式ax2+2x+1>0在R上恒成立.若命题p是真命题,命题q是假命题,求实数a的取值范围.分析 分别求出命题p和命题q为真命题时a的取值范围,结合命题p是真命题,命题q是假命题,可得答案.
解答 解:命题p为真命题时,1-a>1即a<0.…(2分)
命题q:不等式ax2+2x-1<0在R上恒成立,
当a=0时,不符合题意;
当a>0时,
∵ax2+2x-1>0在R上恒成立,
∴△=4-4a<0,
∴a>1.
命题q真时a>1. …(8分)
又命题q是假命题,
∴a≤1.
综上,命题p是真命题,命题q是假命题时,实数a的取值范围为(-∞,0).…(12分)
点评 本题以命题的真假判断与应用为载体,考查了指数函数的图象和性质,恒成立问题,难度中档.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.执行如图所不的程序框图.输出的结果为( )

| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
20.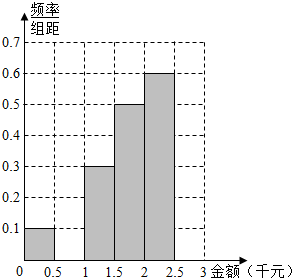 眼下网购成为一种重要的购物方式,某班同学对2015年11月11日在淘宝店网购情况进行了调查,随机抽查了该市当天60名网友的网购金额情况,得到如下数据统计表:
眼下网购成为一种重要的购物方式,某班同学对2015年11月11日在淘宝店网购情况进行了调查,随机抽查了该市当天60名网友的网购金额情况,得到如下数据统计表:
若网购金额超过2千元的顾客定义为“网购达人”,网购金额不超过2千元的顾客定义为“非网购达人”,已知“非网购达人”与“网购达人”人数比恰好为3:2.
(Ⅰ)试确定x,y,p,q的值,并将频率分布直方图补充完整.
(Ⅱ)假设同一组中的每个数据可用该组区间的中点值代替,试估计样本中60名网友的购物金额的平均数.
 眼下网购成为一种重要的购物方式,某班同学对2015年11月11日在淘宝店网购情况进行了调查,随机抽查了该市当天60名网友的网购金额情况,得到如下数据统计表:
眼下网购成为一种重要的购物方式,某班同学对2015年11月11日在淘宝店网购情况进行了调查,随机抽查了该市当天60名网友的网购金额情况,得到如下数据统计表:| 组号 | 网购金额(单位:千元) | 频数 | 频率 |
| 1 | (0,0.5] | 3 | 0.05 |
| 2 | (0.5,1] | x | p |
| 3 | (1,1.5] | 9 | 0.15 |
| 4 | (1.5,2] | 15 | 0.25 |
| 5 | (2,2.5] | 18 | 0.30 |
| 6 | (2.5,3] | y | q |
| 合计 | 60 | 1.00 |
(Ⅰ)试确定x,y,p,q的值,并将频率分布直方图补充完整.
(Ⅱ)假设同一组中的每个数据可用该组区间的中点值代替,试估计样本中60名网友的购物金额的平均数.
7.已知直线(3a+2)x+(1-4a)y+8=0与(5a-2)x+(a+4)y-7=0垂直,则实数a=( )
| A. | 0 | B. | 1 | C. | 0或1 | D. | 0或-1 |
17.篮球运动员乙在某几场比赛中得分的茎叶图如图所示,则他在这几场比赛中得分的中位数为( )

| A. | 26 | B. | 27 | C. | 26.5 | D. | 27.5 |
