题目内容
16．设一四棱锥的体积为V，那么由各棱中点连线所组成的十面体的体积为$\frac{5V}{8}$．分析 作出直观图，则十面体的体积为四棱锥的体积减去5个小棱锥的体积．根据相似比及三角形的面积公式得出小棱锥的体积．使用作差法求出十面体的体积．
解答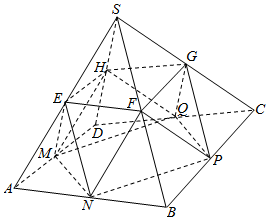 
解：设四棱锥S-ABCD的底面积为S，高为h，则V=$\frac{1}{3}Sh$．
∴S四边形EFGH=$\frac{1}{4}S$，
∴S△AMN+S△CPQ=$\frac{1}{4}S$，S△BPN+S△DMQ=$\frac{1}{4}S$，
∴V棱锥S-EFGH=$\frac{1}{3}$•S四边形EFGH$•\frac{1}{2}h$=$\frac{1}{3}×\frac{S}{4}×\frac{h}{2}=\frac{V}{8}$．
V棱锥E-AMN+V棱锥G-CPQ=$\frac{1}{3}•$（S△AMN+S△CPQ）$•\frac{1}{2}h$=$\frac{V}{8}$，
V棱锥H-DMQ+V棱锥F-BNP=$\frac{1}{3}•$（S△BPN+S△DMQ）$•\frac{1}{2}h$=$\frac{V}{8}$．
∴十面体的体积为V-V棱锥S-EFGH-V棱锥E-AMN-V棱锥G-CPQ-V棱锥H-DMQ-V棱锥F-BNP=$\frac{5V}{8}$．
故答案为：$\frac{5V}{8}$．
点评 本题考查了棱锥的结构特征，棱锥的体积计算，属于中档题．
练习册系列答案
尖子生新课堂课时作业系列答案
英才计划同步课时高效训练系列答案
相关题目
6．设点P（x，y）是曲线a|x|+b|y|=1（a＞0，b＞0）上的动点，且满足$\sqrt{{x^2}+{{（y+1）}^2}}+\sqrt{{x^2}+{{（y-1）}^2}}≤2\sqrt{2}$，则a+$\sqrt{2}$b的取值范围为（ ）
| A． | [2，+∞） | B． | [1，2] | C． | [1，+∞） | D． | （0，2] |
7．若实数x，y满足$\left\{\begin{array}{l}x-y+1≥0\\ x+y≥0\\ x≤0\end{array}\right.$，则z=|x+2y-3|的最小值为（ ）
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
4．
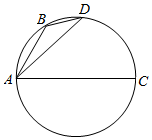如图，B、D是以AC为直径的圆上的两点，其中$AB=\sqrt{t+1}$，$AD=\sqrt{t+2}$，则$\overrightarrow{AC}$$•\overrightarrow{BD}$=（ ）
如图，B、D是以AC为直径的圆上的两点，其中$AB=\sqrt{t+1}$，$AD=\sqrt{t+2}$，则$\overrightarrow{AC}$$•\overrightarrow{BD}$=（ ）| A． | 1 | B． | 2 | C． | t | D． | 2t |
1．已知函数f（x）=2sin2（ωx+$\frac{π}{6}$）（ω＞0）在区间[0，$\frac{π}{2}$]内单调递增，则ω的最大值是（ ）
| A． | $\frac{2}{3}$ | B． | 1 | C． | $\frac{3}{2}$ | D． | 2 |