题目内容

14．设整数a使得关于x的一元二次方程5x2-5ax+26a-143=0的两个根都是整数，则a的值是18．

分析 先因式分解得到（5x-26）（5x-5a+26）=39，即可得到只存在39=1×39或39×1或3×13或13×3或四种情况，分别计算判断即可．

解答 解：∵5x2-5ax+26a-143=0⇒25x2-25ax+（130a-262）-39=0，
即（5x-26）（5x-5a+26）=39，
∵x，a都是整数，故（5x-26）、（5x-5a+26）都分别为整数，
而只存在39=1×39或39×1或3×13或13×3或四种情况，
①当5x-26=1、5x-5a+26=39联立解得a=2.8不符合，
②当5x-26=39、5x-5a+26=1联立解得a=18，
③当5x-26=3、5x-5a+26=13联立解得a=8.4不符合，
④当5x-26=13、5x-5a+26=3联立解得a=12.4不符合，
∴当a=18时，方程为5x2-90x+325=0两根为13、-5．
故答案为：18．

点评 本题考查了方程根的问题，关键是分类讨论，属于基础题．

练习册系列答案
相关题目
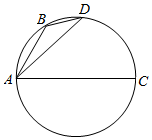4．如图，B、D是以AC为直径的圆上的两点，其中$AB=\sqrt{t+1}$，$AD=\sqrt{t+2}$，则$\overrightarrow{AC}$$•\overrightarrow{BD}$=（　　）
A．1B．2C．tD．2t
5．已知椭圆C的中心为坐标原点O，焦点在x轴上，长轴长为$2\sqrt{2}$，离心率为$\frac{\sqrt{2}}{2}$，斜率为k，直线l与y轴交于点P（0，m），与椭圆C交于相异两点A、B，且$\overrightarrow{AP}=3\overrightarrow{PB}$．
（I）求椭圆方程；
（Ⅱ）求m的取值范围．
2．设f（x）是定义在R上的偶函数，当x≤0时，f（x）=2x2-x，则f（1）=3．
9．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{\sqrt{2}}{2}$，左、右焦点分别为F1，F2．G为椭圆上异于长轴端点的一点，若△GF1F2的面积为2，且其内切圆半径为2-$\sqrt{2}$．
（1）求椭圆C的方程；
（2）直线l：y=k（x-1）（k＜0）与椭圆C相交于A、B两点，点P（3，0），记直线PA，PB的斜率分别为k1、k2，当$\frac{{k}_{1}{k}_{2}}{k}$取得最大值时，求直线l的方程．
19．已知函数f（x）=logacos（2x-$\frac{π}{3}$）（其中a＞0，且a≠1）．
（1）求它的定义域；
（2）求它的单调区间；
（3）判断它的奇偶性；
（4）判断它的周期性，如果是周期函数，求出它的周期．
6．在△ABC中，B=$\frac{π}{3}$，3sinC=8sinA，且△ABC的面积为6$\sqrt{3}$，则△ABC的周长为18．
3．设椭圆$C：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$，若直线l：y=-$\frac{\sqrt{3}}{3}$x+1经过椭圆C的右焦点及上顶点．
（l）求椭圆C的方程；
（2）设直线x=my+1与椭圆C交于A，B两点，点A关于x轴的对称点为A′（A′与B不重合），则直线A′B与x轴是否交于一个定点？若是，请写出定点坐标，并证明你的结论；若不是，请说明理由．
4．现有5张卡片，其正反两面分别写有0与1、2与3、4与5、6与7、8与9，用这五涨卡片可以组成不同的四位数的个数为4536．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网