题目内容
17．
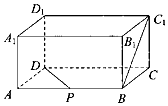如图，在长方体ABCD-A1B1C1D1中，AB=2，BC=1，BB1=1，P是AB的中点，则异面直线BC1与PD所成角等于（ ）| A． | 30° | B． | 45° | C． | 60° | D． | 90° |
分析 根据题意，取CD的中点Q，连接BQ，C1Q，得出BQ∥PD，∠C1BQ是异面直线BC1与PD所成角，利用等边三角形求出∠C1BQ的值即可．
解答 解：长方体ABCD-A1B1C1D1中，AB=2，BC=1，BB1=1，
取CD的中点Q，连接BQ，C1Q，
∵P是AB的中点，∴BQ∥PD，
∴∠C1BQ是异面直线BC1与PD所成角，
如图所示；
△C1BQ中，C1B=BQ=C1Q=$\sqrt{2}$，
∴∠C1BQ=60°，
即异面直线BC1与PD所成角等于60°．
故选：C．
点评 本题考查了异面直线所成的角的作法与计算问题，是基础题目．
练习册系列答案
相关题目
7．数列{an}的通项公式为${a_n}={n^2}+kn$，那么k≥-2是{an}为递增数列的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
2．已知全集U={1，3，5，7}，集合M={1，a-5}，M⊆U，∁UM={5，7}，则a的值为（ ）
| A． | 2 | B． | 8 | C． | -2 | D． | -8 |
6．已知点P是△ABC所在平面内一点，且$\overrightarrow{PA}$=-2$\overrightarrow{PB}$，在△ABC内任取一点Q，则Q落在△APC内的概率为（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{2}{3}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{2}$ |