题目内容
已知函数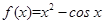 ,则
,则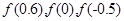 的大小关系是( )
的大小关系是( )
A.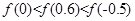 | B.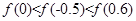 |
C.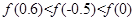 | D.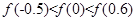 |
B
解析试题分析:∵f(-x)=f(x)∴f(x)为偶函数
∴f(-0.5)=f(0.5)∵f′(x)=2x+sinx,
则函数f(x)在[0,0.6]上单调递增,所以f(0)<f(0.5)<f(0.6),
即f(0)<f(-0.5)<f(0.6).
考点:利用导数研究函数的单调性;函数奇偶性的性质.
点评:解决函数的单调性问题,常利用导数作为解决的工具:导函数大于0时函数递增;导函数小于0时函数递减.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
由直线 ,x=2,曲线
,x=2,曲线 及x轴所围图形的面积为( )
及x轴所围图形的面积为( )
A. | B. | C. | D. |
函数 的导函数
的导函数 的图象与x轴所围
的图象与x轴所围
成的封闭图形的面积为( )
A. 1n2 1n2 | B. 1n2 1n2 | C. 1n2 1n2 | D. 1n2 1n2 |
已知对任意实数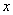 ,有
,有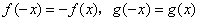 ,且
,且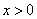 时,
时,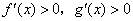 ,则
,则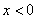 时
时
A.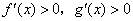 | B.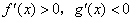 |
C.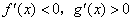 | D.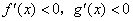 |
点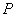 是曲线
是曲线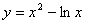 上任意一点, 则点
上任意一点, 则点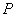 到直线
到直线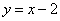 的距离的最小值是( )
的距离的最小值是( )
| A.1 | B.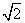 | C.2 | D.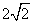 |
已知曲线y= x2-2上一点P
x2-2上一点P ,则过点P的切线的方程是( )
,则过点P的切线的方程是( )
A.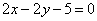 | B.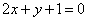 |
C.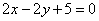 | D.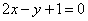 |
函数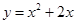 在
在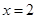 处的切线的斜率为( )
处的切线的斜率为( )
A.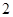 | B. | C. | D.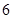 |
若曲线 在点
在点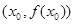 处的切线方程为
处的切线方程为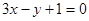 ,则( )
,则( )
A.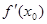 <0 <0 | B.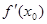 =0 =0 | C.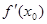 >0 >0 | D.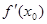 不存在 不存在 |
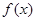 的导函数
的导函数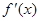 的图象如图所示,则函数
的图象如图所示,则函数

