题目内容
点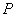 是曲线
是曲线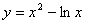 上任意一点, 则点
上任意一点, 则点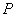 到直线
到直线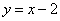 的距离的最小值是( )
的距离的最小值是( )
| A.1 | B.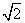 | C.2 | D.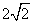 |
B
解析试题分析:求出平行于直线y=x-2且与曲线y=x2-lnx相切的切点坐标,再利用点到直线的距离公式可得结论。解:设P(x,y),则y′=2x-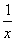 (x>0),令2x-
(x>0),令2x-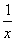 =1,则(x-1)(2x+1)=0,∵x>0,∴x=1,∴y=1,即平行于直线y=x+2且与曲线y=x2-lnx相切的切点坐标为(1,1),由点到直线的距离公式可得d=
=1,则(x-1)(2x+1)=0,∵x>0,∴x=1,∴y=1,即平行于直线y=x+2且与曲线y=x2-lnx相切的切点坐标为(1,1),由点到直线的距离公式可得d=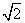 ,故选B.
,故选B.
考点:导数的运用
点评:本题考查导数知识的运用,考查点到直线的距离公式,考查学生的计算能力,属于基础题.

练习册系列答案
相关题目
设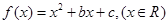 ,且满足
,且满足 ,对任意正实数
,对任意正实数 ,下面不等式恒成立的是( )
,下面不等式恒成立的是( )
A.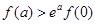 | B.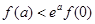 |
C.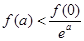 | D.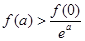 |
曲线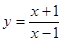 在点
在点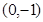 处的切线方程为( )
处的切线方程为( )
A.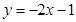 | B.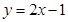 | C.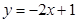 | D.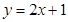 |
若曲线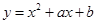 在点
在点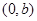 处的切线方程是
处的切线方程是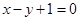 ,则( )
,则( )
A.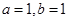 | B.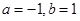 |
C.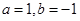 | D.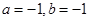 |
已知函数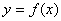 在
在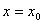 处可导,则
处可导,则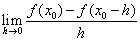 等于
等于
A.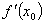 | B.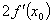 | C.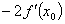 | D.0 |
已知函数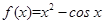 ,则
,则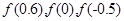 的大小关系是( )
的大小关系是( )
A.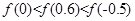 | B.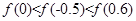 |
C.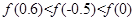 | D.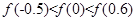 |
由曲线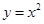 与
与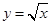 的边界所围成区域的面积为
的边界所围成区域的面积为
A.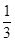 | B.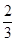 | C.1 | D.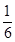 |
设函数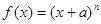 ,其中
,其中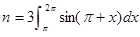 ,
,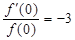 ,则
,则 的展开式中
的展开式中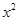 的系数为( )
的系数为( )
A.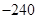 | B.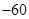 | C.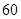 | D.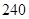 |
设曲线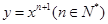 在点(1,1)处的切线与x轴的交点的横坐标为
在点(1,1)处的切线与x轴的交点的横坐标为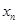 ,则
,则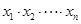 的值为
的值为
A.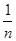 | B.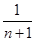 | C.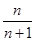 | D.1 |