题目内容
由直线
，x=2，曲线
及x轴所围图形的面积为（ ）
A． | B． | C． | D． |
D
解析试题分析：由题意画出图形，再利用定积分即可求得．
解：如图，面积S=
=ln2-ln
=2ln2．故选D．
考点：定积分的运用
点评：本题主要考查定积分求面积，属于基础题。
练习册系列答案
相关题目
若曲线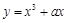
在坐标原点处的切线方程是
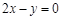，则实数
（ ）
| A．1 | B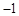． | C．2 | D． |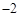
曲线
在
处的切线的倾斜角是（ ）
A． | B． | C． | D． |
已知
，
是
的导函数，即
，
，…，
，
，则
A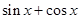． | B． |
C． | D． |
设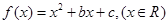
，且满足
，对任意正实数
，下面不等式恒成立的是（ ）
A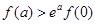． | B． |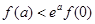
C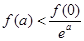． | D． |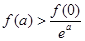
已知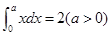
,则
的值为（ ）
| A．1 | B．2 | C．3 | D．4 |
在曲线
的所有切线中，斜率最小的切线方程为 （ ）
A． | B． | C． | D． |
设曲线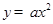
在点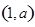
处的切线与直线
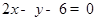平行，则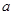
＝（ ）
A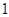． ； | B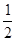． ； | C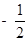． ； | D． |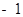
已知函数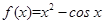
，则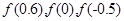
的大小关系是（ ）
A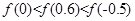． | B． |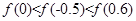
C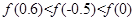． | D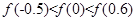． |