题目内容
已知曲线y= x2-2上一点P
x2-2上一点P ,则过点P的切线的方程是( )
,则过点P的切线的方程是( )
A.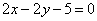 | B.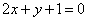 |
C.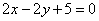 | D.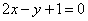 |
A
解析试题分析:根据题意,由于曲线y= x2-2上一点P
x2-2上一点P ,则y’=x,那么可知在点P处的导数值为1,可知点斜式方程得到y+
,则y’=x,那么可知在点P处的导数值为1,可知点斜式方程得到y+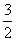 =(x-1),化简变形可知得到为
=(x-1),化简变形可知得到为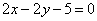 ,选A
,选A
考点:导数的几何意义
点评:主要是考查了导数的几何意义的运算,求解切线方程属于基础题。

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
已知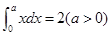 ,则
,则 的值为( )
的值为( )
| A.1 | B.2 | C.3 | D.4 |
一质点做直线运动,由始点经过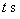 后的距离为
后的距离为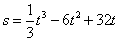 ,则速度为
,则速度为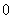 的时刻是( )
的时刻是( )
A.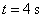 | B.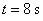 | C.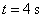 与 与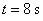 | D.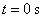 与 与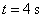 |
设函数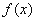 在
在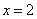 处导数存在,则
处导数存在,则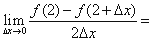 ( )
( )
A.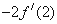 | B.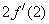 | C.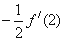 | D.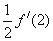 |
已知函数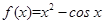 ,则
,则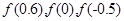 的大小关系是( )
的大小关系是( )
A.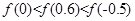 | B.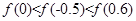 |
C.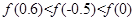 | D.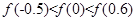 |
若存在过点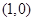 的直线与曲线
的直线与曲线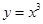 和
和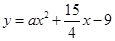 都相切,则
都相切,则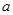 等于
等于
A.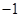 或 或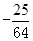 | B.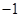 或 或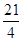 | C.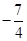 或 或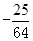 | D.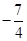 或 或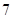 |
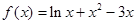 的极大值点是( )
的极大值点是( )
A.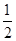 | B.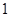 | C.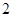 | D.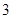 |
若定义在R上的函数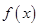 的导函数是
的导函数是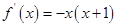 ,则函数
,则函数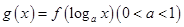 的单调递减区间是( )
的单调递减区间是( )
A.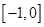 | B.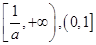 | C.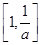 | D.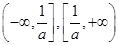 |
 与
与 是定义在R上的两个可导函数,若
是定义在R上的两个可导函数,若 ,
, 满足
满足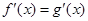 ,则
,则 与
与 满足
满足
A.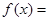  | B.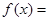 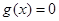 |
C.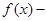  为常数函数 为常数函数 | D.  为常数函数 为常数函数 |