题目内容
(本题满分16分)
已知圆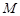 :
: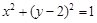 ,设点
,设点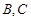 是直线
是直线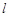 :
: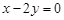 上的两点,它们的横坐标分别
上的两点,它们的横坐标分别
是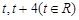 ,
,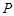 点的纵坐标为
点的纵坐标为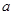 且点
且点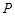 在线段
在线段 上,过
上,过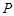 点作圆
点作圆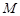 的切线
的切线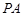 ,切点为
,切点为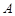
(1)若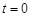 ,
,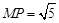 ,求直线
,求直线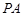 的方程;
的方程;
(2)经过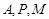 三点的圆的圆心是
三点的圆的圆心是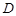 ,
,
①将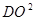 表示成
表示成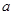 的函数
的函数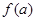 ,并写出定义域.
,并写出定义域.
②求线段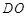 长的最小值
长的最小值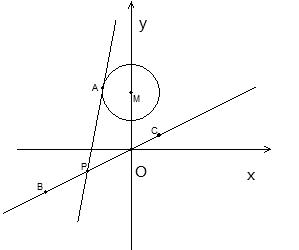
已知圆
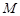 :
: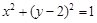 ,设点
,设点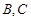 是直线
是直线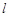 :
: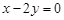 上的两点,它们的横坐标分别
上的两点,它们的横坐标分别是
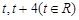 ,
,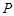 点的纵坐标为
点的纵坐标为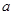 且点
且点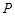 在线段
在线段 上,过
上,过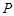 点作圆
点作圆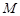 的切线
的切线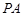 ,切点为
,切点为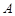
(1)若
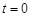 ,
,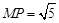 ,求直线
,求直线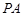 的方程;
的方程;(2)经过
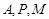 三点的圆的圆心是
三点的圆的圆心是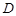 ,
,①将
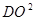 表示成
表示成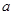 的函数
的函数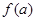 ,并写出定义域.
,并写出定义域.②求线段
 长的最小值
长的最小值
(1)直线PA的方程是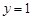 或
或 (2)
(2) .
.
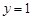 或
或 (2)
(2) .
.本试题主要是考查直线与圆的位置关系的综合运用。
(1)
 解得
解得 或
或 (舍去).
(舍去).
由题意知切线PA的斜率存在,设斜率为k.
所以直线PA的方程为 ,即
,即
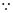 直线PA与圆M相切,
直线PA与圆M相切, ,解得
,解得 或
或
进而得到直线PA的方程是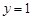 或
或
(2)
 与圆M相切于点A,
与圆M相切于点A,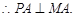
 经过
经过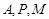 三点的圆的圆心D是线段MP的中点.
三点的圆的圆心D是线段MP的中点. 的坐标是
的坐标是
 (
( )
)
对于参数t讨论得到最值。
(1)
 解得
解得 或
或 (舍去).
(舍去).
由题意知切线PA的斜率存在,设斜率为k.
所以直线PA的方程为 ,即
,即
 直线PA与圆M相切,
直线PA与圆M相切, ,解得
,解得 或
或
 直线PA的方程是
直线PA的方程是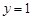 或
或
(2)①
 与圆M相切于点A,
与圆M相切于点A,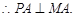
 经过
经过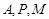 三点的圆的圆心D是线段MP的中点.
三点的圆的圆心D是线段MP的中点.
 的坐标是
的坐标是
 (
( )
)
②当 ,即
,即 时,
时,
当 ,即
,即 时,
时,
当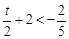 ,即
,即 时
时
则 .
.
(1)

 解得
解得 或
或 (舍去).
(舍去).
由题意知切线PA的斜率存在,设斜率为k.
所以直线PA的方程为
 ,即
,即
 直线PA与圆M相切,
直线PA与圆M相切, ,解得
,解得 或
或
进而得到直线PA的方程是
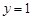 或
或
(2)

 与圆M相切于点A,
与圆M相切于点A,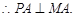
 经过
经过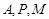 三点的圆的圆心D是线段MP的中点.
三点的圆的圆心D是线段MP的中点. 的坐标是
的坐标是
 (
( )
)对于参数t讨论得到最值。
(1)

 解得
解得 或
或 (舍去).
(舍去).
由题意知切线PA的斜率存在,设斜率为k.
所以直线PA的方程为
 ,即
,即
 直线PA与圆M相切,
直线PA与圆M相切, ,解得
,解得 或
或
 直线PA的方程是
直线PA的方程是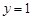 或
或
(2)①

 与圆M相切于点A,
与圆M相切于点A,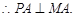
 经过
经过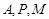 三点的圆的圆心D是线段MP的中点.
三点的圆的圆心D是线段MP的中点. 的坐标是
的坐标是
 (
( )
)②当
 ,即
,即 时,
时,
当
 ,即
,即 时,
时,
当
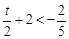 ,即
,即 时
时
则
 .
.
练习册系列答案
相关题目
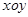 中O是坐标原点,
中O是坐标原点,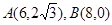 ,圆
,圆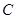 是
是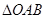 的外接圆,过点(2,6)的直线为
的外接圆,过点(2,6)的直线为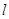 。
。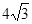 ,求直线
,求直线 ,点
,点 是圆
是圆 上任意一点,则
上任意一点,则 面积的最大值是
面积的最大值是 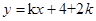 与曲线
与曲线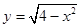 有两个交点,则
有两个交点,则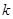 的取值范围是( )
的取值范围是( )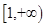



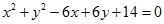 关于直线
关于直线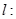
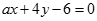 对称,则直线的斜率是( )
对称,则直线的斜率是( ) 


 的直线
的直线 与曲线
与曲线 有公共点,则直线
有公共点,则直线



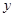 轴相切,圆心在直线
轴相切,圆心在直线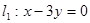 上,且在直线
上,且在直线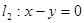 上截得的弦长为
上截得的弦长为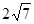 ,求圆C的方程.
,求圆C的方程. 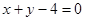 上,则
上,则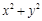 的最小值是___________.
的最小值是___________.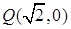 ,并且与定圆
,并且与定圆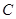 :
: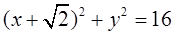 (圆心为C)相切.
(圆心为C)相切.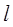 经过圆
经过圆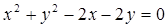 的圆心M,交动圆圆心P的轨迹于A、B两点.是否存在常数k,使得
的圆心M,交动圆圆心P的轨迹于A、B两点.是否存在常数k,使得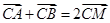 ?如果存在,求出
?如果存在,求出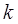 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.