题目内容
如图,在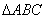 中,
中,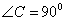 ,
,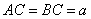 ,点
,点 在边
在边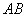 上,
上,
设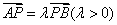 ,过点
,过点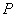 作
作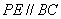 交
交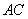 于
于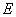 ,作
,作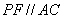 交
交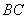 于
于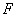 。沿
。沿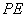 将
将
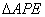 翻折成
翻折成 使平面
使平面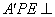 平面
平面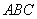 ;沿
;沿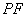 将
将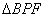 翻折成
翻折成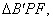 使平面
使平面
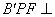 平面
平面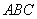 。
。
(1)求证: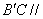 平面
平面 ;
;
(2)是否存在正实数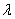 ,使得二面角
,使得二面角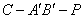 的大小为
的大小为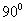 ?若存在,求出
?若存在,求出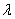 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
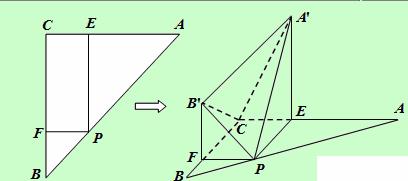
解:(1)法一:以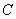 为原点,
为原点, 所在直线为
所在直线为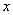 轴,
轴, 所在直线为
所在直线为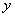 轴,过C且垂直于平面
轴,过C且垂直于平面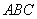 的直线为
的直线为 轴,建立空间直角坐标系,如图,
轴,建立空间直角坐标系,如图,
则 设
设 ,
,
由


 ,
,
从而

于是 ,
, ,
,
平面 的一个法向量为
的一个法向量为 ,
,
又 ,
, ,从而
,从而 平面
平面 。
。
法二:因为 ,
, 平面
平面 ,所以
,所以 平面
平面 ,因为平面
,因为平面 平面
平面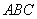 ,且
,且 ,所以
,所以 平面
平面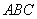 .同理,
.同理, 平面
平面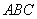 ,所以
,所以 ,从而
,从而 平面
平面 .所以平面
.所以平面 平面
平面 ,从而
,从而 平面
平面 。
。
(2)解:由(1)中解法一有: ,
, ,
,
 。可求得平面
。可求得平面 的一个法向量
的一个法向量 ,平面
,平面 的一个法向量
的一个法向量 ,由
,由 ,即
,即 ,又
,又 ,
, ,由于
,由于 ,
,
所以不存在正实数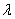 ,使得二面角
,使得二面角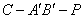 的大小为
的大小为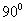 。
。

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
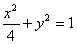 的上、下顶点分别为A、B,点P在椭圆C上且异于点A、B,直线AP、PB与直线l:y=-2分别交于点M、N.
的上、下顶点分别为A、B,点P在椭圆C上且异于点A、B,直线AP、PB与直线l:y=-2分别交于点M、N.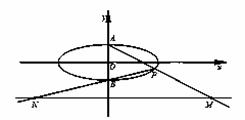
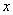 ,符号[
,符号[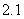 ]=2;[
]=2;[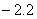 ]=
]=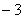 , 这个函数[
, 这个函数[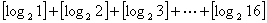 的值为
的值为 B.
B. C.
C. D.
D.

 平面
平面 ,四边形
,四边形 是正方形,四边形
是正方形,四边形 ,
, 是
是 的中点,则
的中点,则 与平面
与平面 所成角的正弦值为___________。
所成角的正弦值为___________。
 ( )
( ) B.
B.  C.
C.  D.
D. 
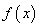 为偶函数,且当
为偶函数,且当 时,
时, ,又函数
,又函数 ,则函数
,则函数 在
在 上的零点的个数为( )个。
上的零点的个数为( )个。  B.
B.  C.
C.  D.
D. 
 上定义运算
上定义运算 :
: ,若
,若 对任意实数
对任意实数 都成立,则实数
都成立,则实数 的取值范围是
的取值范围是  ,则
,则 的值是 .
的值是 .