题目内容
5．已知等比数列{an}前n项和为Sn，且S4=16，S8=17，则公比q=$±\frac{1}{2}$．分析 利用等比数列的前n项和公式直接求解．
解答 解：∵等比数列{an}前n项和为Sn，且S4=16，S8=17，
∴$\frac{{S}_{8}}{{S}_{4}}=\frac{{a}_{1}（1-{q}^{8}）}{{a}_{1}（1-{q}^{4}）}$=1+q4=$\frac{17}{16}$，
解得q=$±\frac{1}{2}$．
故答案为：$±\frac{1}{2}$．
点评 本题考查等比数列的公比的求法，是基础题，解题时要认真审题，注意等比数列的性质的合理运用．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
6．某校高三共有男生400名，从所有高三男生中随机抽取20名男生测量身高（单位：cm）作为样本，得到频率分布表与频率分布直方图1（部分）如表：
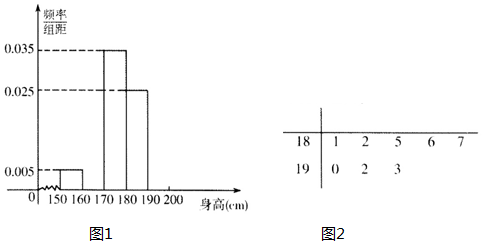
（Ⅰ）求n1、n2、f1、f2；
（Ⅱ）试估计身高不低于180cm的该校高三男生人数，并说明理由；
（Ⅲ）从样本中不低于180cm的男生身高，绘制成茎叶图（图2）；
现从身高不低于185cm的男生中任取3名参加选拔性测试，求至少有两位身高不低于190cm的概率．
| 分组 | 频数 | 频率 |
| [150，160） | 1 | |
| [160，170） | n1 | f1 |
| [170，180） | n2 | f2 |
| [180，190） | 5 | |
| [190，200] | 3 |
（Ⅰ）求n1、n2、f1、f2；
（Ⅱ）试估计身高不低于180cm的该校高三男生人数，并说明理由；
（Ⅲ）从样本中不低于180cm的男生身高，绘制成茎叶图（图2）；
现从身高不低于185cm的男生中任取3名参加选拔性测试，求至少有两位身高不低于190cm的概率．
15．
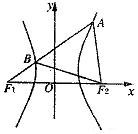如图，F1，F2分别是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（{a＞0，b＞0}）$的左、右焦点，过F1的直线l与双曲线分别交于点A，B，若△ABF2为等边三角形，则双曲线的渐近线的斜率为（ ）
如图，F1，F2分别是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（{a＞0，b＞0}）$的左、右焦点，过F1的直线l与双曲线分别交于点A，B，若△ABF2为等边三角形，则双曲线的渐近线的斜率为（ ）| A． | ±$\sqrt{3}$ | B． | ±2 | C． | $±\sqrt{6}$ | D． | ±$\sqrt{2}$ |