题目内容

11．二项式${（9x-\frac{1}{{3\root{3}{x}}}）^9}$的展开式中x的系数等于（　　）
A．84B．24C．6D．-24

分析 Tr+1=${∁}_{9}^{r}（9x）^{9-r}（-\frac{1}{3\root{3}{x}}）^{r}$=99-r$（-\frac{1}{3}）^{r}$${∁}_{9}^{r}$${x}^{9-\frac{4r}{3}}$，令$9-\frac{4r}{3}$=1，解得r即可得出．

解答 解：Tr+1=${∁}_{9}^{r}（9x）^{9-r}（-\frac{1}{3\root{3}{x}}）^{r}$=99-r$（-\frac{1}{3}）^{r}$${∁}_{9}^{r}$${x}^{9-\frac{4r}{3}}$，
令$9-\frac{4r}{3}$=1，解得r=6．
∴二项式${（9x-\frac{1}{{3\root{3}{x}}}）^9}$的展开式中x的系数=${9}^{3}×（-\frac{1}{3}）^{6}$${∁}_{9}^{6}$=84．
故选：A．

点评 本题考查了二项式定理的应用，考查了推理能力与计算能力，属于基础题．

练习册系列答案
相关题目
1．已知点P在直线x+3y-2=0上，点Q在直线x+3y+6=0上，线段PQ的中点为M（x0，y0），且y0＜x0+2，则$\frac{y_0}{x_0}$的取值范围是（　　）
A．[-$\frac{1}{3}$，0）B．（-$\frac{1}{3}$，0）C．（-$\frac{1}{3}$，+∞）D．（-∞，-$\frac{1}{3}$）∪（0，+∞）
2．已知P，Q分别是直线l：x-y-2=0和圆C：x2+y2=1上的动点，圆C与x轴正半轴交于点A（1，0），则|PA|+|PQ|的最小值为（　　）
A．$\sqrt{2}$B．2C．$\sqrt{5}-1$D．$\frac{\sqrt{2}+\sqrt{10}}{2}$-1
19．设Sn为数列{an}的前n项和，且Sn=（-1）nan-$\frac{1}{{2}^{n}}$．
（I）求a1，a2，a3；
（Ⅱ）求数列{an}的通项公式．
6．在极坐标系中，已知点$A（2，\frac{π}{4}）$，圆C的方程为$ρ=4\sqrt{2}sinθ$（圆心为点C），求直线AC的极坐标方程．
16．已知圆心为H的圆x2+y2+2x-15=0和定点A（1，0），B是圆上任意一点，线段AB的中垂线l和直线BH相交于点M，当点B在圆上运动时，点M的轨迹记为椭圆，记为C．
（Ⅰ）求C的方程；
（Ⅱ）过点A作两条相互垂直的直线分别与椭圆C相交于P，Q和E，F，求$\overrightarrow{PE}•\overrightarrow{QF}$的取值范围．
3．在椭圆E：$\frac{x^2}{4}+{y^2}=1$上任取一点P，过P作x轴的垂线PD，D为垂足，点M满足$\overrightarrow{DM}=2\overrightarrow{DP}$，点M的轨迹为曲线C．
（1）求曲线C的方程；
（2）过点B1（0，1）作直线交椭圆E于A1，B1，交曲线C于A2，B2，当|A1B1|最大时，求|A2B2|．
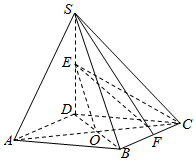20．如图，四棱锥S-ABCD底面是正方形，SD⊥平面ABCD，SD=AD=2，点E是SD的中点，F是BC线段上的点，O是AC与BD的交点．
（Ⅰ）求证：OE∥平面SBC；
（Ⅱ）若直线SF与平面ABCD所成角的正弦值为$\frac{2}{3}$，求二面角C-OE-F的大小．
1．已知：x2+x+1=0，则x5+$\frac{1}{{x}^{5}}$的值为（　　）
A．$\frac{1+\sqrt{3}i}{2}$B．$\frac{1-\sqrt{3}i}{2}$C．1D．-1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网