题目内容
已知: 、
、 、
、 是同一平面内的三个向量,其中
是同一平面内的三个向量,其中 =(1,2)
=(1,2)
(1)若| |=
|= ,且
,且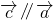 ,求
,求 的坐标;
的坐标;
(2)若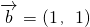 ,且
,且 与
与 的夹角为锐角,求实数λ的取值范围.
的夹角为锐角,求实数λ的取值范围.
解:(1)∵ =(1,2),
=(1,2),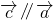 ,故可设
,故可设  =λ
=λ =(λ,2λ),由|
=(λ,2λ),由| |=
|= ,可得 λ2+4λ2=20,
,可得 λ2+4λ2=20,
解得 λ=±2,
∴ =(2,4)或(-2,-4).
=(2,4)或(-2,-4).
(2)∵ =(1,2),
=(1,2),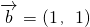 ,
,
∴ =(λ+1,λ+2),
=(λ+1,λ+2),
∵ 与
与 的夹角为锐角,
的夹角为锐角,
∴ •(
•(  )>0,
)>0,
∴λ+1+2λ+4>0,λ> .
.
而当 与
与 共线且方向相同时,(λ+1,λ+2)=k(1,2),k>0,
共线且方向相同时,(λ+1,λ+2)=k(1,2),k>0,
解得 λ=0,
故λ的取值范围为( ,0)∪(0,+∞).
,0)∪(0,+∞).
分析:(1)设 =λ
=λ =(λ,2λ),由|
=(λ,2λ),由| |=
|= ,可得 λ2+4λ2=20,解方程求得λ 值.
,可得 λ2+4λ2=20,解方程求得λ 值.
(2)求出 =(λ+1,λ+2),由
=(λ+1,λ+2),由  与
与 的夹角为锐角可得
的夹角为锐角可得  •(
•(  )>0,解得λ的范围,
)>0,解得λ的范围,
而当 与
与 共线且方向相同时,求出对应的λ的值,从而得到λ的取值范围.
共线且方向相同时,求出对应的λ的值,从而得到λ的取值范围.
点评:本题主要考查两个向量的数量积公式,两个向量共线的性质,两个向量坐标形式的运算,两个向量夹角公式的应用,属于中档题.
 =(1,2),
=(1,2),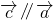 ,故可设
,故可设  =λ
=λ =(λ,2λ),由|
=(λ,2λ),由| |=
|= ,可得 λ2+4λ2=20,
,可得 λ2+4λ2=20,解得 λ=±2,
∴
 =(2,4)或(-2,-4).
=(2,4)或(-2,-4).(2)∵
 =(1,2),
=(1,2),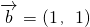 ,
,∴
 =(λ+1,λ+2),
=(λ+1,λ+2),∵
 与
与 的夹角为锐角,
的夹角为锐角,∴
 •(
•(  )>0,
)>0,∴λ+1+2λ+4>0,λ>
 .
.而当
 与
与 共线且方向相同时,(λ+1,λ+2)=k(1,2),k>0,
共线且方向相同时,(λ+1,λ+2)=k(1,2),k>0,解得 λ=0,
故λ的取值范围为(
 ,0)∪(0,+∞).
,0)∪(0,+∞).分析:(1)设
 =λ
=λ =(λ,2λ),由|
=(λ,2λ),由| |=
|= ,可得 λ2+4λ2=20,解方程求得λ 值.
,可得 λ2+4λ2=20,解方程求得λ 值.(2)求出
 =(λ+1,λ+2),由
=(λ+1,λ+2),由  与
与 的夹角为锐角可得
的夹角为锐角可得  •(
•(  )>0,解得λ的范围,
)>0,解得λ的范围,而当
 与
与 共线且方向相同时,求出对应的λ的值,从而得到λ的取值范围.
共线且方向相同时,求出对应的λ的值,从而得到λ的取值范围.点评:本题主要考查两个向量的数量积公式,两个向量共线的性质,两个向量坐标形式的运算,两个向量夹角公式的应用,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 、
、 、
、
 是同一平面内的三个向量,其中
是同一平面内的三个向量,其中 ,且
,且 ,求
,求 且
且 与
与 垂直,求
垂直,求 .
. 、
、 、
、 是同一平面内的三个向量,其中
是同一平面内的三个向量,其中 =(1,2)
=(1,2) |
| ,且
,且 ,求
,求 的坐标;
的坐标; |=
|= 且
且 与
与 垂直,求
垂直,求 与
与 、
、 、
、 是同一平面内的三个向量,其中
是同一平面内的三个向量,其中 |
| ,且
,且 ,求
,求 且
且 与
与 垂直,求
垂直,求 .
.