题目内容
1.化简:$\sqrt{(1+si{n}^{2}\frac{x}{2})^{2}+(1-si{n}^{2}\frac{x}{2})^{2}-4si{n}^{2}\frac{x}{2}}$=$\sqrt{2}co{s}^{2}\frac{x}{2}$.分析 利用完全平方公式化简,利用正弦函数的值域开方后,利用平方关系化简即可.
解答 解:$\sqrt{{(1+si{n}^{2}\frac{x}{2})}^{2}+{(1-si{n}^{2}\frac{x}{2})}^{2}-4si{n}^{2}\frac{x}{2}}$=$\sqrt{2si{n}^{4}\frac{x}{2}-4si{n}^{2}\frac{x}{2}+2}$
=$\sqrt{2(si{n}^{4}\frac{x}{2}-2si{n}^{2}\frac{x}{2}+1)}$=$\sqrt{2(si{n}^{2}\frac{x}{2}-1)^{2}}$=$\sqrt{2}$(1-$si{n}^{2}\frac{x}{2}$)
=$\sqrt{2}co{s}^{2}\frac{x}{2}$,
故答案为:$\sqrt{2}co{s}^{2}\frac{x}{2}$.
点评 本题考查同角三角函数的平方关系,完全平方公式,以及正弦函数的性质的应用,注意化简前后式子的符号.

练习册系列答案
相关题目
11.执行如图所示的程序框图,若输出的$S=\frac{25}{24}$,则判断框内填入的条件可以是( )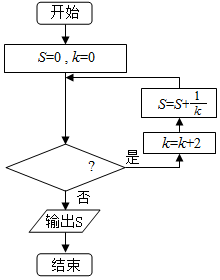

| A. | k≥7 | B. | k>7 | C. | k≤8 | D. | k<8 |
13.若a>b.则下列各式正确的是( )
| A. | a•lgx>b•lgx | B. | ax2>bx2 | C. | a2>b2 | D. | a•2x>b•2x |