题目内容
18．已知等差数列{an}满足a2+a4=4，a3+a5=10，则它的前6项的和S6=21．分析 直接由题意列式，求得首项和公差d，再由前6项和得答案
解答 解：由题意．等差数列{an}满足a2+a4=4，a3+a5=10，
则a1+d+a1+3d=4…①，
a1+2d+a1+4d=10…②，
由①②解得：a1=-4，d=3，
那么：${S}_{6}={6a}_{1}+\frac{6×5}{2}×3$=21．
故答案为：21．
点评 本题考查了等差数列的通项公式，考查了等差数列的前n项和，是基础题．
练习册系列答案
相关题目
9．已知抛物线y2=4x的准线与x轴交于点P，过点P且斜率为k（k＞0）的直线l与抛物线交于A，B两点，F为抛物线的焦点，若|FB|=2|FA|，则k的值为（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{{\sqrt{2}}}{3}$ | C． | $\frac{2}{3}$ | D． | $\frac{{2\sqrt{2}}}{3}$ |
13．
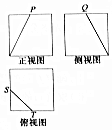一个几何体的三视图是如图所示的边长为2的正方形，其中P，Q，S，T为各边的中点，则此几何体的表面积是（ ）
一个几何体的三视图是如图所示的边长为2的正方形，其中P，Q，S，T为各边的中点，则此几何体的表面积是（ ）| A． | 21 | B． | $\frac{43}{2}$ | C． | $\frac{45}{2}$ | D． | 23 |
3．在△ABC中，若$a=\sqrt{6}$，b=4，B=2A，则sinA的值为（ ）
| A． | $\frac{{\sqrt{6}}}{3}$ | B． | $\frac{{\sqrt{6}}}{6}$ | C． | $\frac{{2\sqrt{3}}}{6}$ | D． | $\frac{{\sqrt{3}}}{3}$ |
7．已知x∈（0，π），且cos（2x-$\frac{π}{2}$）=sin2x，则tan（x-$\frac{π}{4}$）等于（ ）
| A． | $\frac{1}{3}$ | B． | -$\frac{1}{3}$ | C． | 3 | D． | -3 |