题目内容
9．已知抛物线y2=4x的准线与x轴交于点P，过点P且斜率为k（k＞0）的直线l与抛物线交于A，B两点，F为抛物线的焦点，若|FB|=2|FA|，则k的值为（ ）| A． | $\frac{1}{3}$ | B． | $\frac{{\sqrt{2}}}{3}$ | C． | $\frac{2}{3}$ | D． | $\frac{{2\sqrt{2}}}{3}$ |
分析 设出A，B的坐标，再设出AB的方程，联立直线方程和抛物线方程，由焦半径结合|FA|=3|FB|，求得A的坐标，代入两点求斜率公式得答案．
解答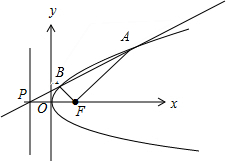 
解：设A（x1，y1），B（x2，y2），
由已知2|FA|=|FB|，得：x2+1=2（x1+1），即x2=2x1+1，①
∵P（-1，0），则AB的方程：y=kx+k，
与y2=4x联立，得：k2x2+（2k2-4）x+k2=0，则x1x2=1，②
由①②得x1=$\frac{1}{2}$，则A（2，2$\sqrt{2}$），
∴k=$\frac{2\sqrt{2}-0}{2+1}$=$\frac{2\sqrt{2}}{3}$，
故选：D．
点评 本题主要考查了抛物线的简单性质．考查了直线与抛物线的关系及焦点弦的问题．常需要利用抛物线的定义来解决．
练习册系列答案
相关题目
3．下列命题中，不是公理的是（ ）
| A． | 平行于同一条直线的两条直线平行 | |
| B． | 如果一条直线上的两点在一个平面内，那么这条直线在此平面内 | |
| C． | 如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线 | |
| D． | 如果两个角的两边分别平行，则这两个角相等或互补 |
20．已知集合A={1，2，3，4}，B={2，3，4，5}，则A∪B等于（ ）
| A． | {2，4} | B． | {1，5} | C． | {2，3，4} | D． | {1，2，3，4，5} |
14．函数$f（x）=\frac{{\sqrt{-lnx}}}{{{x^2}-1}}$的定义域为（ ）
| A． | （-∞，1） | B． | （0，1） | C． | （0，1] | D． | （-∞，-1）∪（-1，1） |
1．设集合A={1，2，3，4}，B={x|x2≤4}，则A∩B=（ ）
| A． | {1，2} | B． | {0，1} | C． | {0，1，2} | D． | {1，2，3，4} |