题目内容
13.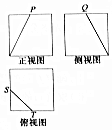 一个几何体的三视图是如图所示的边长为2的正方形,其中P,Q,S,T为各边的中点,则此几何体的表面积是( )
一个几何体的三视图是如图所示的边长为2的正方形,其中P,Q,S,T为各边的中点,则此几何体的表面积是( )| A. | 21 | B. | $\frac{43}{2}$ | C. | $\frac{45}{2}$ | D. | 23 |
分析 由已知中的三视图,可知该几何体是一个边长为2的正方体切去了底面是边长为1是直角三角形,高是2的三棱锥,累加各个面的面积可得,几何体的表面积.
解答 解:根据三视图可知:该几何体是一个边长为2的正方体切去了底面是边长为1是直角三角形,高是2的三棱锥,(如图),切去了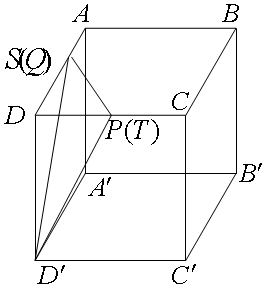 D′-DPS三棱锥,
D′-DPS三棱锥,
由题意:P,Q,S,T为各边的中点,即五边形的面积$S=\frac{1}{2}(2+1)×1+1×2$=$\frac{7}{2}$
3个正方形的面积S=2×2×3=12.
斜面三角形D′PS的边上:ST=$\sqrt{2}$,D′S=D′P=$\sqrt{5}$
∴斜面三角形D′PS的面积$S=\frac{3}{2}$,
两个梯形的面积$S=\frac{1}{2}×(1+2)×2×2$=6.
累加各个面的面积可得几何体的表面积${S}_{总}=\frac{7}{2}+12+\frac{3}{2}+6=23$.
故选D.
点评 本题考查的知识点是由三视图求表面积,解决本题的关键是得到该几何体的形状.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
6.集合A={0,1,2},B={x|x=3-2a,a∈A},则A∩B=( )
| A. | {1} | B. | {1,2} | C. | {0,1,2} | D. | ∅ |
1.设集合A={1,2,3,4},B={x|x2≤4},则A∩B=( )
| A. | {1,2} | B. | {0,1} | C. | {0,1,2} | D. | {1,2,3,4} |
8.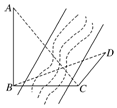 如图,测量河对岸的旗杆高AB时,选与旗杆底B在同一水平面内的两个测点C与D.测得∠BCD=75°,∠BDC=60°,CD=2米,并在点C测得旗杆顶A的仰角为60°,则旗杆高AB为( )
如图,测量河对岸的旗杆高AB时,选与旗杆底B在同一水平面内的两个测点C与D.测得∠BCD=75°,∠BDC=60°,CD=2米,并在点C测得旗杆顶A的仰角为60°,则旗杆高AB为( )
 如图,测量河对岸的旗杆高AB时,选与旗杆底B在同一水平面内的两个测点C与D.测得∠BCD=75°,∠BDC=60°,CD=2米,并在点C测得旗杆顶A的仰角为60°,则旗杆高AB为( )
如图,测量河对岸的旗杆高AB时,选与旗杆底B在同一水平面内的两个测点C与D.测得∠BCD=75°,∠BDC=60°,CD=2米,并在点C测得旗杆顶A的仰角为60°,则旗杆高AB为( )| A. | 10米 | B. | 2$\sqrt{6}$米 | C. | $2\sqrt{3}$米 | D. | $3\sqrt{2}$米 |
5.若方程x2+(m+2)x+m+5=0只有负根,则m的取值范围是( )
| A. | m≥4 | B. | -5<m≤-4 | C. | -5≤m≤-4 | D. | -5<m<-2 |
2.复数z=$\frac{(i-1)^{2}+4}{i+1}$的虚部为( )
| A. | -1 | B. | -3 | C. | 1 | D. | 2 |
 如图,动物园要建造一面靠墙的两间相同的矩形熊猫居室,如果可供建造围墙的材料总长是30m.
如图,动物园要建造一面靠墙的两间相同的矩形熊猫居室,如果可供建造围墙的材料总长是30m.