题目内容
如图,在三棱锥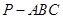 中,
中, 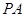 、
、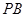 、
、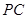 两两垂直, 且
两两垂直, 且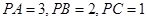 .设
.设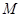 是底面
是底面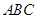 内一点,定义
内一点,定义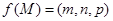 ,其中
,其中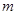 、
、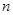 、
、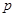 分别是三棱锥M-PAB、 三棱锥M-PBC、三棱锥M-PCA的体积.若
分别是三棱锥M-PAB、 三棱锥M-PBC、三棱锥M-PCA的体积.若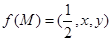 ,且
,且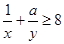 恒成立,则正实数
恒成立,则正实数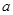 的最小值为___ ___.
的最小值为___ ___.
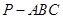 中,
中, 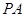 、
、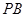 、
、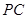 两两垂直, 且
两两垂直, 且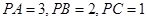 .设
.设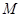 是底面
是底面 内一点,定义
内一点,定义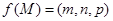 ,其中
,其中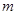 、
、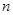 、
、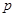 分别是三棱锥M-PAB、 三棱锥M-PBC、三棱锥M-PCA的体积.若
分别是三棱锥M-PAB、 三棱锥M-PBC、三棱锥M-PCA的体积.若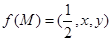 ,且
,且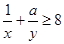 恒成立,则正实数
恒成立,则正实数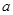 的最小值为___ ___.
的最小值为___ ___.
1
试题分析:∵PA、PB、PC两两垂直,且PA=3.PB=2,PC=1.
 ,即
,即
 ,
,解得
 ,所以正实数a的最小值为1。
,所以正实数a的最小值为1。点评:本题主要考查了棱锥的体积,同时考查了基本不等式的运用,是题意新颖的一道题目,属于中档题.

练习册系列答案
相关题目
 ,
, ,
,
 是平面,
是平面, 是直线,给出下列命题,其中正确的命题的个数是( )
是直线,给出下列命题,其中正确的命题的个数是( ) ,则
,则
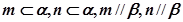 ,则
,则
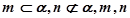 是异面直线,那么
是异面直线,那么 与
与 相交
相交 ,且
,且 ,则
,则 且
且 .
. 的底面边长为4,高为3,在正三棱锥内任取一点
的底面边长为4,高为3,在正三棱锥内任取一点 ,使得
,使得 的概率是( )
的概率是( )



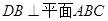 ,
,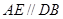 ,
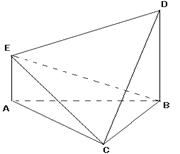
,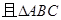 是边长为2的等边三角形,
是边长为2的等边三角形,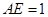 ,CD与平面ABDE所成角的正弦值为
,CD与平面ABDE所成角的正弦值为 .
.
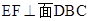 ,若存在,求线段DF的长度,若不存在,说明理由;
,若存在,求线段DF的长度,若不存在,说明理由;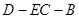 的平面角的余弦值.
的平面角的余弦值.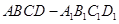 中,
中, ,点
,点 为
为 的中点,点
的中点,点 在
在 上,若
上,若 平面
平面 ,则
,则 ________.
________.
 中,
中,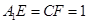 .
.
 与
与 所成角的余弦值;
所成角的余弦值; 与平面
与平面 所成的锐二面角的余弦值.
所成的锐二面角的余弦值. BAD=90°,PA
BAD=90°,PA 底面ABCD,且PA=AD=AB=2BC=2,M、N分别为PC、PB的中点.
底面ABCD,且PA=AD=AB=2BC=2,M、N分别为PC、PB的中点.
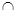 β=m,n与α、β所成的角相等,则m⊥n
β=m,n与α、β所成的角相等,则m⊥n