题目内容
如图,正方体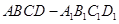 中,
中, ,点
,点 为
为 的中点,点
的中点,点 在
在 上,若
上,若 平面
平面 ,则
,则 ________.
________.
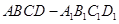 中,
中, ,点
,点 为
为 的中点,点
的中点,点 在
在 上,若
上,若 平面
平面 ,则
,则 ________.
________.

试题分析:根据题意可知,由于正方体
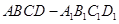 中,
中, ,点
,点 为
为 的中点,点
的中点,点 在
在 上,那么结合
上,那么结合 平面
平面 ,则可知根据线面平行的性质可知,EF//AC,则可致电F为CD的中点,因此根据正方体棱长为2,则AC=2
,则可知根据线面平行的性质可知,EF//AC,则可致电F为CD的中点,因此根据正方体棱长为2,则AC=2 ,
,
 ,故答案为
,故答案为 。
。点评:解决该试题的管家式将EF转化为AC的长度的比例关系来求解,属于基础题,分析问题和解决问题的能力。

练习册系列答案
相关题目

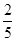 附近,那么点A和点C到直线BD的距离之比约为
附近,那么点A和点C到直线BD的距离之比约为 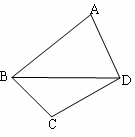




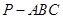 中,
中, 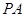 、
、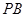 、
、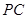 两两垂直, 且
两两垂直, 且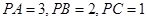 .设
.设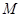 是底面
是底面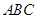 内一点,定义
内一点,定义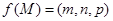 ,其中
,其中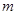 、
、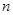 、
、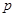 分别是三棱锥M-PAB、 三棱锥M-PBC、三棱锥M-PCA的体积.若
分别是三棱锥M-PAB、 三棱锥M-PBC、三棱锥M-PCA的体积.若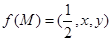 ,且
,且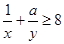 恒成立,则正实数
恒成立,则正实数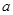 的最小值为___ ___.
的最小值为___ ___.
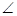 ABC=60
ABC=60 ,EC
,EC 面ABCD,FA
面ABCD,FA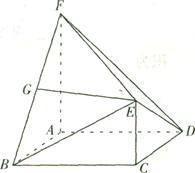

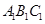 中,
中,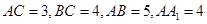 ,点
,点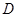 是
是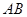 的中点.
的中点. 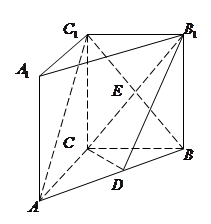
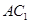 ∥平面
∥平面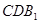 ;
;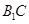 所成的角的余弦值;
所成的角的余弦值;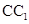 与平面
与平面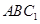 所成角的正弦值;
所成角的正弦值;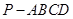 中,
中,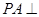 底面
底面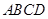 ,
,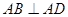 ,
,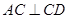 ,
,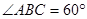 ,
,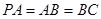 ,
,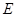 是
是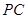 的中点。
的中点。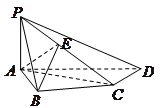
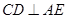 ;
;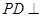 平面
平面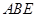 ;
;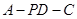 的正切值.
的正切值.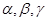 为两两不重合的平面,
为两两不重合的平面,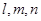 为两两不重合的直线,给出下列四个命题:
为两两不重合的直线,给出下列四个命题: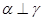 ,
,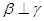 ,则
,则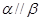 ;
;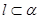 ,则
,则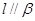 ;
; 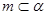 ,
,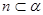 ,
,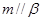 ,
,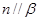 ,则
,则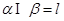 ,
,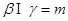 ,
,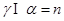 ,
,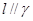 ,则
,则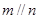 。
。