题目内容
若锐角α、β满足(1+ tanα)(1+
tanα)(1+ tanβ)=4,则α+β=________.
tanβ)=4,则α+β=________.

分析:把已知的等式左边利用多项式的乘法法则化简后,即可得到tanα+tanβ与tanαtanβ的关系式,把关系式根据两角和的正切函数公式变形后即可得到tan(α+β)的值,根据锐角α、β,求出α+β的范围,利用特殊角的三角函数值即可求出α+β的度数.
解答:由(1+
 tanα)(1+
tanα)(1+ tanβ)=4,
tanβ)=4,可得1+
 (tanα+tanβ)+3tanαtanβ=4,
(tanα+tanβ)+3tanαtanβ=4,即
 (tanα+tanβ)=3(1-tanαtanβ)
(tanα+tanβ)=3(1-tanαtanβ)所以
 =
= ,即tan(α+β)=
,即tan(α+β)= .
.又α+β∈(0,π),
∴α+β=
 .
.故答案为:

点评:此题考查学生灵活运用两角和的正切函数公式化简求值,是一道综合题.解本题的关键是将已知的等式灵活变形.

练习册系列答案
相关题目
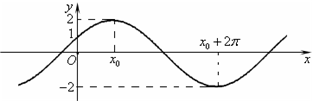
 ,
, ),则f(sinθ)>f(cosθ);
),则f(sinθ)>f(cosθ);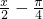 )的图象,只需将y=sin
)的图象,只需将y=sin 的图象向左平移
的图象向左平移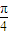 ,
,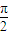 ),则f(sinθ)>f(cosθ);
),则f(sinθ)>f(cosθ);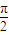 ;
;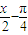 )的图象,只需将y=sin
)的图象,只需将y=sin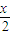 的图象向左平移
的图象向左平移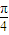 个单位.
个单位.