题目内容
下列命题:
①若f(x)是定义在[-1,1]上的偶函数,且在[-1,0]上是增函数,θ∈( ,
, ),则f(sinθ)>f(cosθ);
),则f(sinθ)>f(cosθ);
②若锐角a、β满足cosa>sinβ则a+β< ;
;
③在△ABC中,“A>B”是“sinA>sinB”成立的充要条件;
④要得到函数y=cos(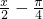 )的图象,只需将y=sin
)的图象,只需将y=sin 的图象向左平移
的图象向左平移 个单位.
个单位.
其中真命题的个数有
- A.1
- B.2
- C.3
- D.4
B
分析:①f(x)是定义在[-1,1]上的偶函数,且在[-1,0]上是增函数,推出f(x)在[0,1]上是减函数,θ∈( ,
, ),则f(sinθ)>f(cosθ),判断正误即可;
),则f(sinθ)>f(cosθ),判断正误即可;
②若锐角a、β,利用 y=sinx在(0, )上单调递增,满足cosa>sinβ,判断a+β<
)上单调递增,满足cosa>sinβ,判断a+β< 的正误;
的正误;
③在△ABC中,“A>B”是“sinA>sinB”成立的充要条件;直接判断即可.
④求出将y=sin 的图象向左平移
的图象向左平移 个单位,得到的解析式判断正误即可.
个单位,得到的解析式判断正误即可.
解答:对于①:由题意知,f(x)在[0,1]上是减函数,又θ∈( ,
, ),∴sinθ>cosθ.∴f(sinθ)<f(cosθ).故①错误;
),∴sinθ>cosθ.∴f(sinθ)<f(cosθ).故①错误;
对于②:锐角α、β满足cosα>sinβ,即sin( -α)>sinβ.
-α)>sinβ.
又0< -α<
-α< ,0<β<
,0<β< ,且y=sinx在(0,
,且y=sinx在(0, )上单调递增,
)上单调递增,
∴ -α>β,即α+β<
-α>β,即α+β< .故②正确.
.故②正确.
对于③在△ABC中,“A>B”是“sinA>sinB”成立的充要条件,正确;
过于④将y=sin 的图象向左平移
的图象向左平移 个单位.得到函数y=cos(
个单位.得到函数y=cos( )的图象,不正确;
)的图象,不正确;
故选B
点评:本题是基础题,考查三角函数的基本性质,函数的单调性,对称性,图象的平移等有关知识,考查计算能力,推理判断能力.
分析:①f(x)是定义在[-1,1]上的偶函数,且在[-1,0]上是增函数,推出f(x)在[0,1]上是减函数,θ∈(
 ,
, ),则f(sinθ)>f(cosθ),判断正误即可;
),则f(sinθ)>f(cosθ),判断正误即可;②若锐角a、β,利用 y=sinx在(0,
 )上单调递增,满足cosa>sinβ,判断a+β<
)上单调递增,满足cosa>sinβ,判断a+β< 的正误;
的正误;③在△ABC中,“A>B”是“sinA>sinB”成立的充要条件;直接判断即可.
④求出将y=sin
 的图象向左平移
的图象向左平移 个单位,得到的解析式判断正误即可.
个单位,得到的解析式判断正误即可.解答:对于①:由题意知,f(x)在[0,1]上是减函数,又θ∈(
 ,
, ),∴sinθ>cosθ.∴f(sinθ)<f(cosθ).故①错误;
),∴sinθ>cosθ.∴f(sinθ)<f(cosθ).故①错误;对于②:锐角α、β满足cosα>sinβ,即sin(
 -α)>sinβ.
-α)>sinβ.又0<
 -α<
-α< ,0<β<
,0<β< ,且y=sinx在(0,
,且y=sinx在(0, )上单调递增,
)上单调递增,∴
 -α>β,即α+β<
-α>β,即α+β< .故②正确.
.故②正确.对于③在△ABC中,“A>B”是“sinA>sinB”成立的充要条件,正确;
过于④将y=sin
 的图象向左平移
的图象向左平移 个单位.得到函数y=cos(
个单位.得到函数y=cos( )的图象,不正确;
)的图象,不正确;故选B
点评:本题是基础题,考查三角函数的基本性质,函数的单调性,对称性,图象的平移等有关知识,考查计算能力,推理判断能力.

练习册系列答案
相关题目
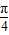 ,
,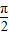 ),则f(sinθ)>f(cosθ);
),则f(sinθ)>f(cosθ);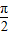 ;
;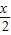 -1,则f(x+π)=f(x)对x∈R恒成立;
-1,则f(x+π)=f(x)对x∈R恒成立;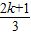 πx-
πx-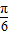 )(k∈N*)在区间[a,a+3]上的值
)(k∈N*)在区间[a,a+3]上的值 出现的次数不小于4次,又不多于8次,则k可以取2和3.
出现的次数不小于4次,又不多于8次,则k可以取2和3.