Question

已知函数f（x）=Asin（ωx+?）(A＞0，ω＞0，|?|＜

π

2

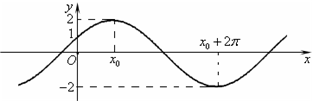
)的图象与y轴的交点为（0，1），它在y轴右侧的第一个最高点和第一个最低点的坐标分别为（x₀，2）何（x₀+2π，-2）．
（Ⅰ）求f（x）的解析式及x₀的值；
（Ⅱ）若锐角θ满足cosθ=

1

3

，求f（4θ）的值．

Answer 1

分析：（Ⅰ）由f（x）的函数图象可知A，由

T

2

=2π可求得ω，再由f（0）=1可求得φ，继而可求得x₀的值；
（Ⅱ）由（Ⅰ）可知f（4θ）=2sin（2θ+

π

6

），由cosθ=

1

3

，θ为锐角可求得sin2θ与cos2θ的值，从而可求得答案．

解答：本题考查由y=Asin（ωx+φ）的部分图象确定其解析式，求φ是关键，也是难点，考查分析与运算能力，属于中档题．

点评：解：（Ⅰ）由f（x）的函数图象知A=2，

T

2

=2π，
∴T=

2π

ω

=4π，
∴ω=

1

2

．
又f（0）=1，即2sinφ=1，
∴sinφ=

1

2

，又|φ|＜

π

2

，
∴φ=

π

6

．
∴f（x）=2sin（

1

2

x+

π

6

）．
又f（x₀）=2sin（

1

2

x₀+

π

6

）=2，
∴sin（

1

2

x₀+

π

6

）=1，
∴由图知

1

2

x₀+

π

6

=

π

2

，
∴x₀=

2π

3

．
（Ⅱ）∵f（x）=2sin（

1

2

x+

π

6

），
∴f（4θ）=2sin（2θ+

π

6

），
又cosθ=

1

3

，θ为锐角，
∴cos2θ=2cos²θ-1=-

7

9

，sin2θ=2sinθcosθ=

4 2

9

，
∴f（4θ）=2sin（2θ+

π

6

），
=2sin2θcos

π

6

+2cos2θsin

π

6

=2×

4 2

9

×

3

2

+2×（-

7

9

）×

1

2

=

4 6 -7

9

．