题目内容
2．某少数民族的刺绣有着悠久的历史，图（1）、（2）、（3）、（4）为她们刺绣最简单的四个图案，这些图案都是由小正方形构成，小正方形数越多刺绣越漂亮；现按同样的规律刺绣（小正方形的摆放规律相同），设第n个图形包含f（n）个小正方形．（Ⅰ）求出f（5）的值；
（Ⅱ）利用合情推理的“归纳推理思想”，归纳出f（n）与f（n-1）之间的关系式，并根据你得到的关系式求出f（n）的表达式．
分析 先分别观察给出正方体的个数为：1，1+4，1+4+8，…总结一般性的规律，将一般性的数列转化为特殊的数列再求解．
解答 解：（Ⅰ）f（5）=41…（4分）
（Ⅱ）因为f（2）-f（1）=4=4×1，f（3）-f（2）=8=4×2，f（4）-f（3）=12=4×3，f（5）-f（4）=16=4×4
由以上规律，所以得出f（n）-f（n-1）=4（n-1）…（8分）
f（n）-f（n-1）=4（n-1）
f（n-1）-f（n-2）=4（n-2）
…f（3）-f（2）=8=4×2
f（2）-f（1）=4=4×1
相加得：f（n）-f（1）=4[1+2+3+…+（n-2）+（n-1）]=$4×\frac{n（n-1）}{2}=2{n^2}-2n$，
∴f（n）=2n2-2n+1…（12分）
点评 本题主要考查归纳推理，其基本思路是先分析具体，观察，总结其内在联系，得到一般性的结论，若求解的项数较少，可一直推理出结果，若项数较多，则要得到一般求解方法，再求具体问题．
练习册系列答案
科学实验活动册系列答案
相关题目
1．已知数列{an}为等比数列，且a3a13+2a82=5π，则cos（a5a11）的值为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | $\frac{\sqrt{2}}{2}$ | D． | -$\frac{1}{2}$ |
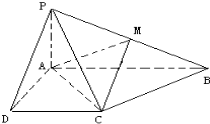如图所示，在四棱锥P-ABCD中，底面ABCD为直角梯形，AB∥CD，∠DAB=90°，PA⊥平面ABCD，且PA=CD=AD=$\frac{1}{2}$AB，M为PB的中点．
10．数列{an}中，${a_n}+{a_{n+2}}=2{a_{n+1}}（{n∈{N^*}}），{a_5}=5$，则有（ ）
| A． | a4•a6=25 | B． | a4•a6≤25 | C． | a4•a6＞25 | D． | a4•a6＜25 |
已知定义在[0，1]上的函数y=f（x），f′（x）为f（x）的导函数，f（x）图象如图，对满足0＜x1＜x2＜1的任意x1，x2，给出下列结论：