题目内容
7. 已知定义在[0,1]上的函数y=f(x),f′(x)为f(x)的导函数,f(x)图象如图,对满足0<x1<x2<1的任意x1,x2,给出下列结论:
已知定义在[0,1]上的函数y=f(x),f′(x)为f(x)的导函数,f(x)图象如图,对满足0<x1<x2<1的任意x1,x2,给出下列结论:①f(x1)-f(x2)>x1-x2;
②x2f(x1)>x1f(x2);
③$\frac{f({x}_{1})+f({x}_{2})}{2}$<f($\frac{{x}_{1}+{x}_{2}}{2}$);
④[f′(x1)-f′(x2)]•(x1-x2)>0.
则下列结论中正确的是②③.
分析 根据题意可作出函数y=f(x)的图象,利用直线的斜率的几何意义,利用数形结合的思想研究函数的单调性与最值即可得到答案.
解答  解:由函数y=f(x)的图象可得,
解:由函数y=f(x)的图象可得,
对于④当0<x1<x2<1时,0<f(x1)<f(x2)<1,
[f(x2)-f(x1)]•(x2-x1)>0,故④错误;
函数y=f(x)在区间[0,1]上的图象如图:
对于①设曲线y=f(x)上两点A(x1,f(x1)),B(x2,f(x2)),
直线AB的斜率kAB=$\frac{f({x}_{2})-f({x}_{1})}{{x}_{2}-{x}_{1}}$<kop=1,
∴f(x2)-f(x1)<x2-x1,故①错误;
对于③,由图可知,koA>koB,即$\frac{f({x}_{1})}{{x}_{1}}$>$\frac{f({x}_{2})}{{x}_{2}}$,0<x1<x2<1,于是有x2f(x1)>x1f(x2),故②正确;
对于④,设AB的中点为R,则R($\frac{{x}_{1}+{x}_{2}}{2}$,$\frac{f({x}_{1})+f({x}_{2})}{2}$),$\widehat{AB}$的中点为S,则S($\frac{{x}_{1}+{x}_{2}}{2}$,f($\frac{{x}_{1}+{x}_{2}}{2}$),
显然有$\frac{f({x}_{1})+f({x}_{2})}{2}$<f($\frac{{x}_{1}+{x}_{2}}{2}$),即③正确.
对于④当0<x1<x2<1时,0<f(x1)<f(x2)<1,[f(x2)-f(x1)]•(x2-x1)>0,故④错误;
综上所述,正确的结论的序号是②③.
故答案为:②③.
点评 本题考查函数的图象,着重考查直线的斜率的几何意义,考察函数的单调性,突出考查作图象的能力与数形结合解决问题的能力,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | $-\frac{3}{2}-\frac{1}{e}$ | B. | $-\frac{3}{2}-\frac{2}{e}$ | C. | $-\frac{3}{4}-\frac{1}{2e}$ | D. | $-1-\frac{1}{e}$ |
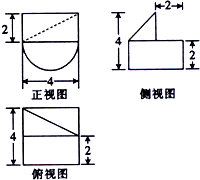
| A. | $\frac{16}{3}$+8π | B. | $\frac{32}{3}$+8π | C. | 16+8π | D. | $\frac{16}{3}$+16π |
| A. | S10≤S9 | B. | S10<S11 | C. | S10=S9 | D. | S10=S11 |
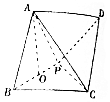 如图,在四棱锥P-ABCD中,底面ABCD是菱形,且AB=$\sqrt{2}$,∠ABC=60°,点A在平面PBC上的射影为PB的中点O,PB⊥AC.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,且AB=$\sqrt{2}$,∠ABC=60°,点A在平面PBC上的射影为PB的中点O,PB⊥AC.