已知$\underset{lim}{△x→0}$$\frac{f({x} {0}-\frac{1}{2}△x)-f}{2△x}$=5.则f′(x0)=( )A．6B．-2C．-$\frac{20}{7}$D．3 题目和参考答案——青夏教育精英家教网—

题目内容

3．已知$\underset{lim}{△x→0}$$\frac{f（{x}_{0}-\frac{1}{2}△x）-f（{x}_{0}+3△x）}{2△x}$=5，则f′（x₀）=（　　）

A．

B．

-2

C．

-$\frac{20}{7}$

D．

分析根据导数的变化率即可求出．

解答解：原式=-$\frac{7}{4}$$\underset{lim}{△x→0}$$\frac{f（{x}_{0}-\frac{1}{2}△x）-f（{x}_{0}+3△x）}{-\frac{7}{2}△x}$=-$\frac{7}{4}$f′（x₀）=5，
∴f′（x₀）=-$\frac{20}{7}$，
故选：C

点评本题主要考查函数在某一点的导数的定义，求一个函数的导数的方法，属于基础题．

练习册系列答案

相关题目

20．点A（2，1）到抛物线y²=ax准线的距离为1，则a的值为（　　）

A．

$-\frac{1}{4}$或$-\frac{1}{12}$

B．

$\frac{1}{4}$或$\frac{1}{12}$

1．运行程序框图，若输出的S的值为$\frac{{{2^9}-1}}{2^9}$，则判断框内的整数a为10．

11．已知直线l₁过直线l₂：x+2y=0与l₃：2x+2y-1=0的交点，与圆x²+y²+2y=0相切，则直线l₁的方程是（　　）

18．数列{a_n}满足a₁=1，a₂=5，a_n+2=2a_n+1-a_n+1
（1）设b_n=a_n+1-a_n，证明{b_n}是等差数列，并求{b_n}的通项公式；
（2）设c_n=tanb_n•tanb_n+1，求数列{c_n}的前n项和S_n．

8．过双曲线$\frac{{x}^{2}}{{a}^{2}}$-y²=1（a＞0）的左焦点作直线l与双曲线交于A，B两点，使得|AB|=4，若这样的直线有且仅有两条，则a的取值范围是（　　）

（0，$\frac{1}{2}$）∪（2，+∞）

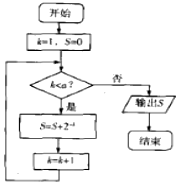
15．如图是一个程序框图，则输出的S的值是（　　）

12．已知实数集R为全集，A={x|log₂（3-x）≤2}，B={x||x-3|≤2}，
（1）求A，B；
（2）求∁_R（A∩B）．

13．已知在等比数列{a_n}中，a₅-a₁=15，a₄-a₂=6，则公比q的所有可能的值为$\frac{1}{2}$或2．

试题分类