题目内容
设函数f（x）=x5+x+sinx，x∈R，则不等式f（x2-2）+f（x）＜0的解集是 ．
考点：奇偶性与单调性的综合
专题：计算题,函数的性质及应用,不等式的解法及应用
分析：运用导数判断函数的单调性，再由奇偶性的定义判断奇偶性，不等式f（x2-2）+f（x）＜0即为f（x2-2）＜-f（x）=f（-x），即有x2-2＜-x，解不等式即可得到解集．
解答：
解：函数f（x）=x5+x+sinx的导数为：
f′（x）=5x4+1+cosx≥0，
则f（x）在R上递增，
又f（-x）=-x5-x+sin（-x）=-（x5+x+sinx）=-f（x），
则f（x）为奇函数，
则不等式f（x2-2）+f（x）＜0即为f（x2-2）＜-f（x）=f（-x），
即有x2-2＜-x，解得，-2＜x＜1．
则解集为（-2，1）．
故答案为：（-2，1）．
f′（x）=5x4+1+cosx≥0，
则f（x）在R上递增，
又f（-x）=-x5-x+sin（-x）=-（x5+x+sinx）=-f（x），
则f（x）为奇函数，
则不等式f（x2-2）+f（x）＜0即为f（x2-2）＜-f（x）=f（-x），
即有x2-2＜-x，解得，-2＜x＜1．
则解集为（-2，1）．
故答案为：（-2，1）．
点评：本题考查函数的奇偶性和单调性的判断和运用，考查不等式的解法，考查运算能力，属于中档题．
练习册系列答案
相关题目
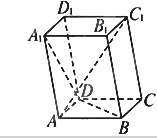已知平行六面体ABCD-A1B1C1D1中，底面ABCD是边长为1的正方形．AA1=2，∠A1AB=∠A1AD=120°．
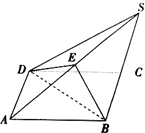如图所示，四边形ABCD是平行四边形，直线SC⊥平面ABCD，E是SA的中点，求证：平面BDE⊥平面ABCD．
如图所示的抛物线y=-