题目内容
10．若不等式x2-ax+b＜0的解集为{x|-1＜x＜3}，则a+b=-1．分析 根据不等式x2-ax+b＜0与对应方程解的情况，利用由根与系数的关系，求出a、b的值．
解答 解：∵不等式x2-ax+b＜0的解集为（-1，3），
∴方程x2-ax+b=0的解-1和3，
由根与系数的关系，得；$\left\{\begin{array}{l}{a=-1+3}\\{b=-1×3}\end{array}\right.$，
∴a=2，b=-3；
∴a+b=-1．
故答案为：-1．
点评 本题考查了一元二次不等式与一元二次方程的应用问题，也考查了根与系数的关系的应用问题，是基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
1．定义2×2矩阵$[\begin{array}{l}{{a}_{1}}&{{a}_{2}}\\{{a}_{3}}&{{a}_{4}}\end{array}]$=a1a4-a2a3，若f（x）=$[\begin{array}{l}{cosx-sinx}&{\sqrt{3}}\\{cos（\frac{π}{2}+2x）}&{cosx+sinx}\end{array}]$，则f（x）（ ）
| A． | 图象关于（π，0）中心对称 | B． | 图象关于直线$x=\frac{π}{2}$对称 | ||
| C． | 在区间$[-\frac{π}{6}，0]$上单调递增 | D． | 周期为π的奇函数 |
1．A是曲线ρ=3cosθ上任意一点，点A到直线ρcosθ=-1距离的最大值为（ ）
| A． | $\frac{5}{2}$ | B． | 3 | C． | 4 | D． | 5 |
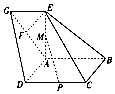如图，四边形ABCD是正方形，且平面ABCD⊥平面ABEG，F是AG上一点，且△ABE与△AEF都是等腰直角三角形，AB=AE，AF=EF．