题目内容
(理)已知正方体ABCD一A1B1C1D1的棱长为1,则BC1与DB1的距离为( )
A. B.
B. C.
C. D.2
D.2
C
【解析】
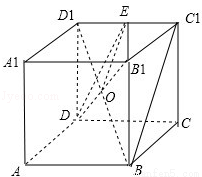
试题分析:连接BD1,BD1∩DB1=O,取C1D1的中点E,连接DE,EB1,则OE∥BC1,可得BC1∥平面DB1E,从而BC1与DB1的距离为BC1与平面DB1E的距离,即C1到平面DB1E的距离,利用等体积可求.
【解析】
连接BD1,BD1∩DB1=O,取C1D1的中点E,连接DE,EB1,则OE∥BC1,
∵BC1?平面DB1E,OE?平面DB1E
∴BC1∥平面DB1E
∴BC1与DB1的距离为BC1与平面DB1E的距离,即C1到平面DB1E的距离
在△DB1E中,DE=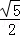 ,EB1=
,EB1=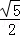 ,DB1=
,DB1=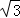 ,EO=
,EO=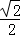 ,
,
∴S△DB1E=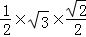 =
=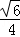
设C1到平面DB1E的距离为d,则由VC1﹣DB1E=VD﹣B1C1E,可得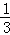 ×
×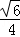 d=
d=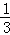 ×
×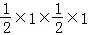
∴d=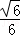
故选C.

练习册系列答案
相关题目
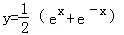 的导数是( )
的导数是( )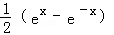 B.
B.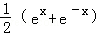 C.ex﹣e﹣x D.ex+e﹣x
C.ex﹣e﹣x D.ex+e﹣x
 B.
B. C.
C. D.
D.
 B.
B. C.
C. D.
D.
 = .
= . ,
, 满足
满足 ,则
,则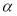 ,条件“直线l与平面α内的无数条直线都垂直”是“直线l与平面α垂直的( ).
,条件“直线l与平面α内的无数条直线都垂直”是“直线l与平面α垂直的( ).