题目内容
2．已知函数y=f（x）=$\frac{1}{\sqrt{x}}$，求f′（x），f′（1）分析 根据函数y=xα的求导公式，求出f（x）的导数并计算f′（1）的值．
解答 解：函数y=f（x）=$\frac{1}{\sqrt{x}}$=${x}^{-\frac{1}{2}}$，
∴f′（x）=-$\frac{1}{2}$${x}^{-\frac{3}{2}}$，
∴f′（1）=-$\frac{1}{2}$．
点评 本题考查了函数y=xα求导公式的应用问题，是基础题目．
练习册系列答案
相关题目
12．下列命题正确的是（ ）
| A． | 如果两个复数的积是实数，那么这两个复数互为共轭复数 | |
| B． | 用反证法证明命题“设a，b为实数，则方程x2+ax+b=0至少有一个实根”时，要做的假设是：方程x2+ax+b=0至多有一个实根 | |
| C． | 在复平面中复数z满足|z|=2的点的轨迹是以原点为圆心，以2为半径的圆 | |
| D． | 等轴双曲线$\frac{x^2}{3}-\frac{y^2}{3}=1$上任意一点到两焦点的距离之差=$2\sqrt{3}$ |
13．不等式x2+2x-3＞0的解集是（ ）
| A． | {x|x＜-3或x＞1} | B． | {x|x＜-1或x＞3} | C． | {x|-1＜x＜3} | D． | {x|-3＜x＜1} |
10．已知集合A={1，2，3}，则“a=3”是“a∈A“的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既充分也不必要条件 |
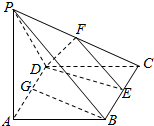如图所示，在四棱柱P-ABCD中，底面ABCD是菱形，∠DAB=60°，侧面PAD为正三角形，其所在平面垂直于底面ABCD，