题目内容
15．抛物线y=4ax2（a≠0）的焦点坐标是$（0，\frac{1}{16a}）$．分析 利用抛物线方程直接求解抛物线的焦点坐标即可．
解答 解：抛物线y=4ax2（a≠0）的标准方程为：x2=$\frac{1}{4a}y$，所以抛物线的焦点坐标为：$（0，\frac{1}{16a}）$．
故答案为：$（0，\frac{1}{16a}）$．
点评 本题考查抛物线的简单性质的应用，是基础题．
练习册系列答案
阳光课堂课时优化作业系列答案
相关题目
6．下列说法错误的是（ ）
| A． | xy≠10是x≠5或y≠2的充分不必要条件 | |
| B． | 若命题p：?x∈R，x2+x+1≠0，则￢p：?x∈R，x2+x+1=0 | |
| C． | 已知随机变量X～N（2，σ2），且P（X≤4）=0.84，则P（X≤0）=0.16 | |
| D． | 相关指数R2越接近1，表示残差平方和越大． |
7．
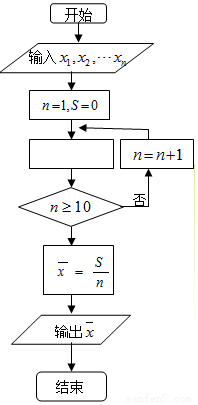如图是求样本x1、x2、…x10平均数$\overline{x}$的程序框图，图中空白框中应填入的内容为（ ）
如图是求样本x1、x2、…x10平均数$\overline{x}$的程序框图，图中空白框中应填入的内容为（ ）| A． | S=S+xn | B． | S=S+$\frac{{x}_{n}}{n}$ | C． | S=S+n | D． | S=S+$\frac{{x}_{n}}{10}$ |