题目内容
11.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左,右焦点分别为F1,F2,点A在双曲线上,且AF2⊥x轴,若△AF1F2的内切圆半价为$({\sqrt{3}-1})a$,则其离心率为( )| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{3}+1$ | D. | $2\sqrt{3}$ |
分析 由题意可得A在双曲线的右支上,由双曲线的定义可得|AF1|-|AF2|=2a,设Rt△AF1F2内切圆半径为r,运用等积法和勾股定理,可得r=c-a,结合条件和离心率公式,计算即可得到所求值.
解答 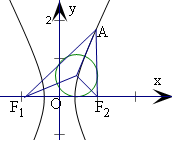 解:由点A在双曲线上,且AF2⊥x轴,
解:由点A在双曲线上,且AF2⊥x轴,
可得A在双曲线的右支上,
由双曲线的定义可得|AF1|-|AF2|=2a,
设Rt△AF1F2内切圆半径为r,
运用面积相等可得S${\;}_{△A{F}_{1}{F}_{2}}$=$\frac{1}{2}$|AF2|•|F1F2|
=$\frac{1}{2}$r(|AF1|+|AF2|+|F1F2|),
由勾股定理可得|AF2|2+|F1F2|2=|AF1|2,
解得r=$\frac{{|{A{F_2}}|+|{{F_1}{F_2}}|-|{A{F_1}}|}}{2}=\frac{2c-2a}{2}=c-a=({\sqrt{3}-1})a$,
$⇒c=\sqrt{3}a$,
则离心率e=$\frac{c}{a}$=$\sqrt{3}$,
故选A.
点评 本题考查双曲线的离心率的求法,注意运用双曲线的定义和三角形的等积法,考查化简整理的运算能力,属于中档题.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
2.已知集合A={x|2x2-7x<0},B={0,1,2,3,4},则(∁RA)∩B=( )
| A. | {0} | B. | {1,2,3} | C. | {0,4} | D. | {4} |
6.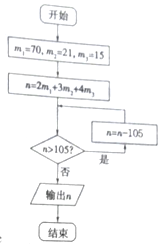 明朝数学家程大位将“孙子定理”(也称“中国剩余定理”)编成易于上口的《孙子歌诀》:三人同行七十稀,五树梅花廿一支,七子团圆正半月,除百零五便得知.已知正整数n被3除余2,被5除余3,被7除余4,求n的最小值.按此歌诀得算法如图,则输出n的结果为( )
明朝数学家程大位将“孙子定理”(也称“中国剩余定理”)编成易于上口的《孙子歌诀》:三人同行七十稀,五树梅花廿一支,七子团圆正半月,除百零五便得知.已知正整数n被3除余2,被5除余3,被7除余4,求n的最小值.按此歌诀得算法如图,则输出n的结果为( )
 明朝数学家程大位将“孙子定理”(也称“中国剩余定理”)编成易于上口的《孙子歌诀》:三人同行七十稀,五树梅花廿一支,七子团圆正半月,除百零五便得知.已知正整数n被3除余2,被5除余3,被7除余4,求n的最小值.按此歌诀得算法如图,则输出n的结果为( )
明朝数学家程大位将“孙子定理”(也称“中国剩余定理”)编成易于上口的《孙子歌诀》:三人同行七十稀,五树梅花廿一支,七子团圆正半月,除百零五便得知.已知正整数n被3除余2,被5除余3,被7除余4,求n的最小值.按此歌诀得算法如图,则输出n的结果为( )| A. | 53 | B. | 54 | C. | 158 | D. | 263 |
16.当双曲线$\frac{x^2}{{{m^2}+8}}-\frac{y^2}{6-2m}=1$的焦距取得最小值时,其渐近线的方程为( )
| A. | y=±x | B. | $y=±\frac{2}{3}x$ | C. | $y=±\frac{1}{3}x$ | D. | $y=±\frac{1}{2}x$ |
3.已知集合P={x∈R,||x|<2},Q={x∈R|-1≤x≤3},则P∩Q=( )
| A. | [-1,2) | B. | (-2,2) | C. | (-2,3] | D. | [-1,3] |
20.已知a,b为实常数,{ci}(i∈N*)是公比不为1的等比数列,直线ax+by+ci=0与抛物线y2=2px(p>0)均相交,所成弦的中点为Mi(xi,yi),则下列说法错误的是( )
| A. | 数列{xi}可能是等比数列 | B. | 数列{yi}是常数列 | ||
| C. | 数列{xi}可能是等差数列 | D. | 数列{xi+yi }可能是等比数列 |
1.函数y=cos2x,x∈R的最小正周期为( )
| A. | $\frac{π}{2}$ | B. | π | C. | 2π | D. | 1 |