题目内容
2.已知集合A={x|2x2-7x<0},B={0,1,2,3,4},则(∁RA)∩B=( )| A. | {0} | B. | {1,2,3} | C. | {0,4} | D. | {4} |
分析 解不等式得集合A,根据补集与交集的定义写出(∁RA)∩B即可.
解答 解:集合A={x|2x2-7x<0}={x|0<x<$\frac{7}{2}$},
∴∁RA={x|x≤0或x≥$\frac{7}{2}$},
又B={0,1,2,3,4},
∴(∁RA)∩B={0,4}.
故选:C.
点评 本题考查了解不等式与集合的运算问题,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.下列说法正确的是( )
| A. | 存在x0∈R,使得$1-{cos^3}{x_0}={log_2}\frac{1}{10}$ | |
| B. | 函数y=sin2xcos2x的最小正周期为π | |
| C. | 函数$y=cos2({x+\frac{π}{3}})$的一个对称中心为$({-\frac{π}{3},0})$ | |
| D. | 角α的终边经过点(cos(-3),sin(-3)),则角α是第三象限角 |
17.已知等差数列{an}的前n项和为Sn,设A(a1009,1),B(2,-1),C(2,2)为坐标平面上三点,O为坐标原点,若向量$\overrightarrow{OA}$与$\overrightarrow{OB}$在向量$\overrightarrow{OC}$方向上的投影相同,则S2017为( )
| A. | -2016 | B. | -2017 | C. | 2017 | D. | 0 |
7.将函数f(x)=sinπx的图象向左平移$\frac{1}{2}$个单位后得到函数g(x)的图象,若f(x)和g(x)在区间[-1,2]上的图象交于A,B,C三点,则△ABC的面积是( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{3\sqrt{2}}{4}$ | C. | $\sqrt{2}$ | D. | $\frac{5\sqrt{2}}{4}$ |
11.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左,右焦点分别为F1,F2,点A在双曲线上,且AF2⊥x轴,若△AF1F2的内切圆半价为$({\sqrt{3}-1})a$,则其离心率为( )
| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{3}+1$ | D. | $2\sqrt{3}$ |
12.若集合A=$\left\{{x|-1<x<1,x∈R}\right\},B=\left\{{x|y=\sqrt{x-2},x∈R}\right\}$,则A∪B=( )
| A. | [0,1) | B. | (-1,+∞) | C. | (-1,1)∪[2,+∞) | D. | ∅ |
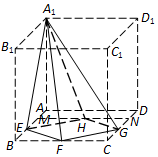 如图,在正方体ABCD-A1B1C1D1中,M、E是AB的三等分点,G、N是CD的三等分点,F、H分别是BC、MN的中点,则四棱锥A1-EFGH的左视图是( )
如图,在正方体ABCD-A1B1C1D1中,M、E是AB的三等分点,G、N是CD的三等分点,F、H分别是BC、MN的中点,则四棱锥A1-EFGH的左视图是( )