题目内容
从椭圆(1)求椭圆的离心率;
(2)若Q是椭圆上任意一点,F2是右焦点,求∠F1QF2的取值范围;
(3)过F1作AB的平行线交椭圆于C、D两点,若|CD|=3,求椭圆的方程.
解:(1)由已知可设M(-c,y),
则有![]() +
+![]() =1.
=1.
∵M在第二象限,∴M(-c,![]() ).
).
又由AB∥OM,可知kAB=kOM.
∴-![]() =-
=-![]() .∴b=c.
.∴b=c.
∴a=![]() b.
b.
∴e=![]() =
=![]() .
.
(2)设|F1Q|=m,|F2Q|=n,则m+n=2a,mn>0.|F1F2|=2c,a2=2c2,
∴cos∠F1QF2=![]()
=![]()
=![]() -1
-1
=![]() -1≥
-1≥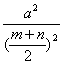 -1
-1
=![]() -1=0.
-1=0.
当且仅当m=n=a时,等号成立.
故∠F1QF2∈[0,![]() ].
].
(3)∵CD∥AB,kCD=-![]() =-
=-![]() .
.
设直线CD的方程为y=-![]() (x+c),
(x+c),
即y=-![]() (x+b).
(x+b).
则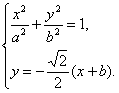 消去y,整理得
消去y,整理得
(a2+2b2)x2+2a2bx-a2b2=0.
设C(x1,y1)、D(x2,y2),∵a2=2b2,
∴x1+x2=-![]() =-
=-![]() =-b,
=-b,
x1·x2=-![]() =-
=-![]() =-
=-![]() .
.
∴|CD|=![]() |x1-x2|
|x1-x2|
=![]() ·
·![]()
=![]() ·
·![]()
=![]() =3.
=3.
∴b2=2,则a2=4.
∴椭圆的方程为![]() +
+![]() =1.
=1.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
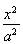
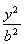
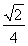
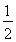
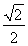
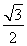
 (a>b>0)上一点M向x轴作垂线恰好通过椭圆的左焦点F1,且它的长轴端点A及短轴端点B的连线AB平行于OM,又Q是椭圆上任一点.
(a>b>0)上一点M向x轴作垂线恰好通过椭圆的左焦点F1,且它的长轴端点A及短轴端点B的连线AB平行于OM,又Q是椭圆上任一点. ,求椭圆方程.
,求椭圆方程.