题目内容
从椭圆 (a>b>0)上一点M向x轴作垂线恰好通过椭圆的左焦点F1,且它的长轴端点A及短轴端点B的连线AB平行于OM,又Q是椭圆上任一点.
(a>b>0)上一点M向x轴作垂线恰好通过椭圆的左焦点F1,且它的长轴端点A及短轴端点B的连线AB平行于OM,又Q是椭圆上任一点.
(1)求椭圆的离心率;
(2)求∠F1QF2的范围;
(3)当QF2⊥AB时,延长QF2与椭圆交于另一点P,若△F1PQ的面积为20 ,求椭圆方程.
,求椭圆方程.
解:(1)∵过点M向x轴作垂线经过左焦点,A(a,0),B(0,b),∴ ,
,
∵AB∥OM,所以kAB=kOM,即 ,从而得到
,从而得到 ,
,
∴离心率 .
.
(2)设|PF1|=m,|PF2|=n
∴ ,
,
又因为 ,所以0≤cos∠F1QF2≤1,所以
,所以0≤cos∠F1QF2≤1,所以 .
.
(3)设P(x1,y1),Q(x2,y2)
∵ ,所以
,所以 ,所以直线F2Q的方程:y=
,所以直线F2Q的方程:y= (x-c)
(x-c)
直线与椭圆联立 ,消元可得5x2-8cx+2c2=0
,消元可得5x2-8cx+2c2=0
∴△=24c2>0, ,
,
由弦长公式可得 ,
,
又因为F1到直线 的距离
的距离 ,
,
因为 ,所以c2=25,b2=25,a2=50,
,所以c2=25,b2=25,a2=50,
所以椭圆的方程为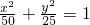 .
.
分析:(1)根据过点M向x轴作垂线经过左焦点,A(a,0),B(0,b),可得M的坐标,利用AB∥OM,即可得到椭圆的离心率;
(2)利用余弦定理,结合基本不等式,可得0≤cos∠F1QF2≤1,从而可确定∠F1QF2的范围;
(3)设P(x1,y1),Q(x2,y2),确定直线F2Q的方程:y= (x-c)与椭圆联立
(x-c)与椭圆联立 ,利用韦达定理,求得弦长公式,F1到直线
,利用韦达定理,求得弦长公式,F1到直线 的距离,根据△F1PQ的面积为20
的距离,根据△F1PQ的面积为20 ,即可得到椭圆的方程.
,即可得到椭圆的方程.
点评:本题考查椭圆的离心率,考查余弦定理的运用,考查基本不等式的运用,考查直线与椭圆的位置关系,考查三角形面积的计算,解题的关键是直线与椭圆联立,确定三角形的面积.
 ,
,∵AB∥OM,所以kAB=kOM,即
 ,从而得到
,从而得到 ,
,∴离心率
 .
.(2)设|PF1|=m,|PF2|=n
∴
 ,
,又因为
 ,所以0≤cos∠F1QF2≤1,所以
,所以0≤cos∠F1QF2≤1,所以 .
.(3)设P(x1,y1),Q(x2,y2)
∵
 ,所以
,所以 ,所以直线F2Q的方程:y=
,所以直线F2Q的方程:y= (x-c)
(x-c)直线与椭圆联立
 ,消元可得5x2-8cx+2c2=0
,消元可得5x2-8cx+2c2=0∴△=24c2>0,
 ,
,由弦长公式可得
 ,
,又因为F1到直线
 的距离
的距离 ,
,因为
 ,所以c2=25,b2=25,a2=50,
,所以c2=25,b2=25,a2=50,所以椭圆的方程为
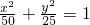 .
.分析:(1)根据过点M向x轴作垂线经过左焦点,A(a,0),B(0,b),可得M的坐标,利用AB∥OM,即可得到椭圆的离心率;
(2)利用余弦定理,结合基本不等式,可得0≤cos∠F1QF2≤1,从而可确定∠F1QF2的范围;
(3)设P(x1,y1),Q(x2,y2),确定直线F2Q的方程:y=
 (x-c)与椭圆联立
(x-c)与椭圆联立 ,利用韦达定理,求得弦长公式,F1到直线
,利用韦达定理,求得弦长公式,F1到直线 的距离,根据△F1PQ的面积为20
的距离,根据△F1PQ的面积为20 ,即可得到椭圆的方程.
,即可得到椭圆的方程.点评:本题考查椭圆的离心率,考查余弦定理的运用,考查基本不等式的运用,考查直线与椭圆的位置关系,考查三角形面积的计算,解题的关键是直线与椭圆联立,确定三角形的面积.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
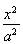
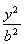
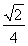
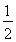
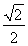
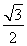
 (a>b>0)上一点M向x轴作垂线恰好通过椭圆的左焦点F1,且它的长轴端点A及短轴端点B的连线AB平行于OM,求椭圆的离心率。
(a>b>0)上一点M向x轴作垂线恰好通过椭圆的左焦点F1,且它的长轴端点A及短轴端点B的连线AB平行于OM,求椭圆的离心率。  (a>b>0)上一点M向x轴作垂线恰好通过椭圆的左焦点F1,且它的长轴端点A及短轴端点B的连线AB平行于OM,又Q是椭圆上任一点.
(a>b>0)上一点M向x轴作垂线恰好通过椭圆的左焦点F1,且它的长轴端点A及短轴端点B的连线AB平行于OM,又Q是椭圆上任一点. ,求椭圆方程.
,求椭圆方程.