题目内容
从椭圆(1)求椭圆的离心率;
(2)若Q是椭圆上任意一点,F2是右焦点,求∠F1QF2的取值范围;
(3)Q为椭圆上的点,当QF2⊥AB时,延长QF2与椭圆交于另一点P,若△F1PQ的面积为20![]() ,求此时椭圆的方程.
,求此时椭圆的方程.
解:(1)∵M点在椭圆上且MF1⊥x轴,
∴M点坐标为(-c,![]() ).
).
又由AB∥OM,可知kAB=kOM,
∴ .∴b=c,a=
.∴b=c,a=![]() b.
b.
∴e=![]() =
=![]() .
.
(2)设|F1Q|=r1,|F2Q|=r2,则r1+r2=2a,r1·r2>0,|F1F2|=2c,a2=2c2,
∴cos∠F1QF2=![]() -1
-1
=![]() ≥
≥ -1=0(当且仅当r1=r2=a时取等号).
-1=0(当且仅当r1=r2=a时取等号).
故∠F1QF2∈[0,![]() ].
].
(3)设直线PQ方程为y=![]() (x-c).
(x-c).
∵a=![]() b,∴y=
b,∴y=![]() (x-c).
(x-c).
因椭圆方程为x2+2y2=2c2,将PQ的方程代入椭圆方程中并整理得5x2-8cx+2c2=0.
∴|PQ|=![]() .
.
设点F1到PQ的距离为h,
则h=![]() c.
c.
∴![]() =
=![]() ×
×![]()
![]() c·
c·![]()
![]() c=
c=![]() c2=20
c2=20![]() ,且c>0.
,且c>0.
∴c=5.于是b=c=5,a=![]() b=5
b=5![]() .
.
因此所求的椭圆方程为![]() =1.
=1.

练习册系列答案
相关题目
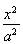
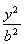
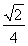
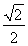
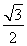
 (a>b>0)上一点M向x轴作垂线恰好通过椭圆的左焦点F1,且它的长轴端点A及短轴端点B的连线AB平行于OM,又Q是椭圆上任一点.
(a>b>0)上一点M向x轴作垂线恰好通过椭圆的左焦点F1,且它的长轴端点A及短轴端点B的连线AB平行于OM,又Q是椭圆上任一点. ,求椭圆方程.
,求椭圆方程.