题目内容
11.求证:任意n∈N*,$\sqrt{e}$<(1+$\frac{1}{{n}^{2}}$)(1+$\frac{2}{{n}^{2}}$)•…•(1+$\frac{n}{{n}^{2}}$)<e成立.分析 要证原不等式成立,可证$\frac{1}{2}$<ln(1+$\frac{1}{{n}^{2}}$)+ln(1+$\frac{2}{{n}^{2}}$)+…+ln(1+$\frac{n}{{n}^{2}}$)<1.构造f(x)=ln(1+x)-x,g(x)=ln(1+x)-$\frac{x}{1+x}$,求得导数判断单调性,再由不等式的性质和等差数列的求和公式,即可得证.
解答 证明:要证任意n∈N*,$\sqrt{e}$<(1+$\frac{1}{{n}^{2}}$)(1+$\frac{2}{{n}^{2}}$)•…•(1+$\frac{n}{{n}^{2}}$)<e成立,
即证$\frac{1}{2}$<ln(1+$\frac{1}{{n}^{2}}$)+ln(1+$\frac{2}{{n}^{2}}$)+…+ln(1+$\frac{n}{{n}^{2}}$)<1.
由f(x)=ln(1+x)-x的导数为f′(x)=$\frac{1}{1+x}$-1=$\frac{-x}{1+x}$<0(x>0),
f(x)在(0,+∞)递减,即有f(x)<f(0)=0,
则ln(1+x)<x,
则ln(1+$\frac{1}{{n}^{2}}$)+ln(1+$\frac{2}{{n}^{2}}$)+…+ln(1+$\frac{n}{{n}^{2}}$)<$\frac{1}{{n}^{2}}$+$\frac{2}{{n}^{2}}$+…+$\frac{n}{{n}^{2}}$=$\frac{\frac{1}{2}n(n+1)}{{n}^{2}}$<1,
又g(x)=ln(1+x)-$\frac{x}{1+x}$的导数为$\frac{1}{1+x}$-$\frac{1}{(1+x)^{2}}$=$\frac{x}{(1+x)^{2}}$>0(x>0),
g(x)在(0,+∞)递增,即有g(x)>g(0)=0,
则ln(1+x)>$\frac{x}{1+x}$,
则ln(1+$\frac{1}{{n}^{2}}$)+ln(1+$\frac{2}{{n}^{2}}$)+…+ln(1+$\frac{n}{{n}^{2}}$)>$\frac{1}{1+{n}^{2}}$+$\frac{2}{2+{n}^{2}}$+…+$\frac{n}{n+{n}^{2}}$
>$\frac{1}{n+{n}^{2}}$+$\frac{2}{n+{n}^{2}}$+…+$\frac{n}{n+{n}^{2}}$=$\frac{\frac{1}{2}n(n+1)}{n+{n}^{2}}$=$\frac{1}{2}$,
即有$\frac{1}{2}$<ln(1+$\frac{1}{{n}^{2}}$)+ln(1+$\frac{2}{{n}^{2}}$)+…+ln(1+$\frac{n}{{n}^{2}}$)<1,
故对任意n∈N*,$\sqrt{e}$<(1+$\frac{1}{{n}^{2}}$)(1+$\frac{2}{{n}^{2}}$)•…•(1+$\frac{n}{{n}^{2}}$)<e成立.
点评 本题考查不等式的证明,考查导数的运用:求单调性,考查不等式的性质和推理能力,属于中档题.

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案| A. | 80种 | B. | 120种 | C. | 480种 | D. | 600种 |
| A. | 15 | B. | 15 | C. | 20 | D. | 6 |
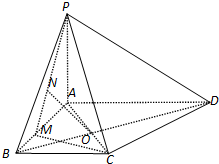 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是梯形,其中AD∥BC,BA⊥AD,AC与BD交于点O,M是AB边上的点,已知PA=AD=4,AB=3,BC=2.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是梯形,其中AD∥BC,BA⊥AD,AC与BD交于点O,M是AB边上的点,已知PA=AD=4,AB=3,BC=2.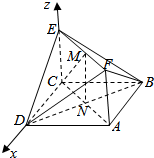 如图所示,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=$\sqrt{2}$,AF=1,M是线段EF的中点,N为AC与BD的交点,求点B到平面CMN的距离.
如图所示,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=$\sqrt{2}$,AF=1,M是线段EF的中点,N为AC与BD的交点,求点B到平面CMN的距离.