题目内容

20．等差数列{an}的前n项之和为Sn，若a2+a6+a10=18，则a6是（　　）
A．15B．15C．20D．6

分析 利用等差数列的通项公式求解．

解答 解：∵等差数列{an}的前n项之和为Sn，a2+a6+a10=18，
∴3a6=18，
∴a6=6．
故选：D．

点评 本题考查等差数列的第6项的求法，是基础题，解题时要认真审题，注意等差数列的性质的合理运用．

练习册系列答案
相关题目
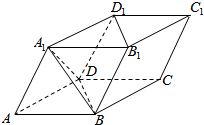10．如图，四棱柱ABCD-A1B1C1D1中，所有棱长均为a，且∠A1AB=∠A1AD=∠DAB=60°，则下列结论正确的是①②④⑤（写出所有正确的结论的编号）．
①平面A1BD∥平面CB1D1；
②四边形BDD1B1为正方形；
③点A到平面BDD1B1的距离为$\frac{\sqrt{3}}{2}$a；
④点A1在平面BDC1上的射影为△BDC1的垂心；
⑤平面A1BD与平面BDD1B1将四棱柱分成从小到大三部分的体积比为1：2：3．
11．求证：任意n∈N*，$\sqrt{e}$＜（1+$\frac{1}{{n}^{2}}$）（1+$\frac{2}{{n}^{2}}$）•…•（1+$\frac{n}{{n}^{2}}$）＜e成立．
8．已知长方体的长、宽、高分别为3、3、4，从长方体的12条棱中任取两条．设ξ为随机变量，当两条棱相交时，ξ=0；当两条棱平行时，ξ的值为两条棱之间的距离；当两条棱异面时，ξ=3．
（1）求概率P（ξ=0）；
（2）求ξ的分布列及数学期望E（ξ）．
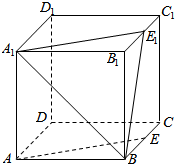15．在棱长为1的正方体ABCD-A1B1C1D1中，E、E1分别是BC和B1C1中点，则：
（1）点B到A1E1的距离为$\frac{\sqrt{30}}{5}$；
（2）点B1到平面A1BE1的距离为$\frac{\sqrt{6}}{6}$；
（3）直线AE到平面A1BE1的距离为$\frac{\sqrt{6}}{6}$；
（4）平面AEC1与平面A1BE1的距离为$\frac{\sqrt{6}}{6}$；
（5）A1在正方体表面上到点E的最短距离为$\frac{\sqrt{13}}{2}$．
5．已知四棱锥P-ABCD中，底面ABCD是平行四边形，点E，F在PC上，且PE：EF：FC=1：1：1，问在PB上是否存在一点M，使平面AEM∥平面BFD，并请说明理由．
12．设函数f（x）=ax3+bx2+cx+d（a≠0），已知关于x的五个方程及其相异实根个数如下表所示：
 方程 根的个数 方程 根的个数
 f（x）-5=0 1 f（x）+4=0 3
 f（x）-3=0 3 f（x）+6=0 1
 f（x）=0 3  
若α为关于f（x）的极大值﹐下列选项中正确的是（　　）
A．-6＜a＜-4B．-4＜a＜0C．0＜a＜3D．3＜a＜5
9．以四棱柱的侧棱为对边的平行四边形有6个．
10．已知a＞0，b＞0，求证：
（1）（a+b）（a-1+b-1）≥4
（2）（a+b）（a2+b2）（a3+b3）≥8a3b3．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网