题目内容
1．
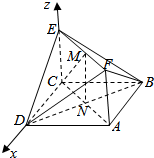如图所示，已知正方形ABCD和矩形ACEF所在的平面互相垂直，AB=$\sqrt{2}$，AF=1，M是线段EF的中点，N为AC与BD的交点，求点B到平面CMN的距离．
分析 证明BN⊥平面CMN，可得BN是点B到平面CMN的距离．
解答 解：由题意，N为AC的中点，MN⊥平面ABCD，
∵BN?平面ABCD，
∴MN⊥BN，
∵BN⊥CN，MN∩CN=N，
∴BN⊥平面CMN，
∴BN是点B到平面CMN的距离，且BN=$\frac{1}{2}$BD=1．
点评 本题考查点B到平面CMN的距离，考查线面垂直的证明，比较基础．
练习册系列答案
相关题目
12．设函数f（x）=ax3+bx2+cx+d（a≠0），已知关于x的五个方程及其相异实根个数如下表所示：
若α为关于f（x）的极大值﹐下列选项中正确的是（ ）
| 方程 | 根的个数 | 方程 | 根的个数 |
| f（x）-5=0 | 1 | f（x）+4=0 | 3 |
| f（x）-3=0 | 3 | f（x）+6=0 | 1 |
| f（x）=0 | 3 |
| A． | -6＜a＜-4 | B． | -4＜a＜0 | C． | 0＜a＜3 | D． | 3＜a＜5 |
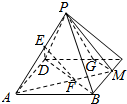如图，已知点P是平行四边形ABCD所在平面外的一点，E，F分别是PA，BD上的点且PE：EA=BF：FD，延长AF交BC于点M．过M作GM∥BD，且GN交CD于G，求证：平面DEF∥平而PGM．